题目内容
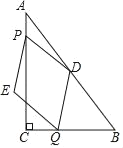
【题目】如图,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)求证:△ABD≌△ACE;
(2)判断△BOC的形状,并说明理由.

【答案】(1)见解析;(2)等腰三角形,理由见解析.
【解析】
(1)由“SAS”可证△ABD≌△ACE;
(2)由全等三角形的性质可得∠ABD=∠ACE,由等腰三角形的性质可得∠ABC=∠ACB,可求∠OBC=∠OCB,可得BO=CO,即可得结论.
证明:(1)∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS);
(2)△BOC是等腰三角形,
理由如下:
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,
∴∠OBC=∠OCB,
∴BO=CO,
∴△BOC是等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】今年是全面建成小康社会和“十三五”规划收官之年,为促进销售,某公司开发了A、B两项新产品,销售前景广阔.已知A、B的成本、售价和每日销量如下表所示:
成本(元/件) | 售价(元/件) | 销量(件/日) | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
根据销售情况,公司对B项产品降价销售,同时对A项产品提价销售,发现B项产品每降价5元就多销售2件,A项产品每提价5元就可少销售1件,要保持每日的总销量不变,设A项产品每天少销售x个,每天总获利为y元.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)要使每天利润不低于208000元,直接写出x的取值范围;
(3)该公司决定每销售一件A产品,就捐给红十字会a(0<a≤100)元作为抗疫基金.当40≤x≤50时,每日的最大利润为237250元,求a的值.