��Ŀ����
����Ŀ��ij��ѧ�С����һ�λ�У���һ����ѧ����������̽����
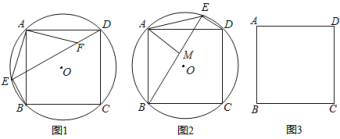
�����ⷢ�֣���ͼ1��������ABCD���ĸ����㶼�ڡ�O�ϣ�����E�ڻ�AB�ϣ�F��DE�ϵ�һ�㣬��DF��BE����˵������ADF�ա�ABE��
����ʽ̽������ͼ2������E�ڻ�AD�ϣ�����A��AM��BE����˵���߶�BE��DE��AM֮�����������ϵ��BE��DE��2AM��
��������⣩��ͼ3����������ABCD�У�CD��2![]() ������P����PD��2���ҡ�BPD��90������ֱ��д����A��BP�ľ��룮
������P����PD��2���ҡ�BPD��90������ֱ��д����A��BP�ľ��룮
���𰸡���1������������2������������3����A��BP�ľ�����![]() ��1��
��1��![]() +1�����ɼ�����
+1�����ɼ�����
��������
��1������֤AD��AB��EB��DF������ֻ��֤����ADF����ABE������ͬ�����Ե�Բ�ܽ���Ȳ��ѵó����Ӷ�֤��ȫ�ȣ�
��2������֤��AEF�ǵ���ֱ�������Σ�����AF��AE����ΪAM��BE������FM��ME��AM��EF��2AM��EF��BEBF��BEDE���ó����ۣ�
��3����PD��2�ɵã���P���Ե�DΪԲ�ģ�2Ϊ�뾶��Բ�ϣ��ɡ�BPD��90���ɵã���P����BDΪֱ����Բ�ϣ���Ȼ����P��������Բ�Ľ��㣬������Բ���������㣬�������������λ�÷ֱ�������ۣ�Ȼ�������ʵ��ĸ����ߣ�������2���н��ۣ����ɽ�����⣮
��1��֤������������ABCD�У�AB��AD��
��ABE���ADE����Ӧ��AE��
���ABE����ADE��
����ADF����ABE��
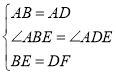 ��
��
���ADF�ա�ABE��SAS����
��2��֤������BE��ȡ��F��ʹBF��DE������AF��
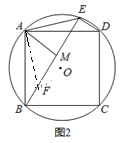
�ɣ�1����ADE�ա�ABF��
��BF��DE��AE��AF����DAE����BAF��
��������ABCD����BAD��90����
���BAF+��DAF��90����
���DAE+��DAF��90����
���EAF��90����
���EAF�ǵ���ֱ�������������Σ�
��AM��BE��
��FM��ME��AM��
��EF��2AM��
��EF��BE��BF��BE��DE��
��BE��DE��2AM��
��3����A��BP�ľ�����![]() ��1��
��1��![]() +1��
+1��
�������£�
��PD��2��
���P���Ե�DΪԲ�ģ�2Ϊ�뾶��Բ�ϣ�
�ߡ�BPD��90����
���P����BDΪֱ����Բ�ϣ�
���P������Բ�Ľ��㣬
�ٵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����BP�ڵ�E����ͼ3�٣�
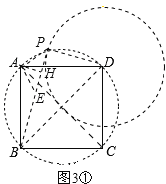
���ı���ABCD�������Σ�
���ADB��45����AB��AD��DC��BC��2![]() ����BAD��90����
����BAD��90����
��BD��4��
��DP��2��
��BP��2![]() ��
��
�ߡ�BPD����BAD��90����
��A��P��D��B����BD
���APB����ADB��45����
���PAE�ǵ���ֱ�������Σ�
�֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP��
���ɣ�2���еĽ��ۿɵã�BP��2AH+PD��
2![]() ��2AH+2��
��2AH+2��
��AH��![]() ��1��
��1��
�ڵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����PB���ӳ����ڵ�E����ͼ3�ڣ�
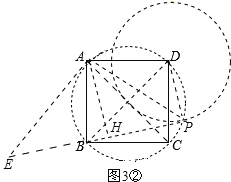
ͬ���ɵã�BP��2AH��PD��
2![]() ��2AH��2��
��2AH��2��
��AH��![]() +1��
+1��
������������A��BP�ľ���Ϊ![]() ��1��
��1��![]() +1��
+1��

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ��ɱ�Ϊ2Ԫ/ǧ�ˣ�ÿ��IJ���![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ����㺯����ϵʽ
��Ԫ/ǧ�ˣ����㺯����ϵʽ![]() �����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������
�����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
���ۼ۸� | 2 | 4 | ���� | 10 |
������� | 12 | 10 | ���� | 4 |
��֪����۲��Ź涨���ۼ۸�![]() ������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
��1��ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ����ע���Ա���
�ĺ�����ϵʽ����ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ��IJ���С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳�������ÿ��IJ��������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ�����
�ٵ�ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����ÿ���õ�����y����Ԫ�������ۼ۸�![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���ڣ�2���������£���![]() Ϊ______Ԫ/ǧ��ʱ������
Ϊ______Ԫ/ǧ��ʱ������![]() �����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���
�����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���![]() Ӧ��Ϊ______Ԫ/ǧ�ˣ�
Ӧ��Ϊ______Ԫ/ǧ�ˣ�
����Ŀ����֦����������������ˣ�ũ��Ʒ��Դ��Ϊ�ḻ����������â��Զ�����Ϲ�ȴ���У�ijˮ���깺��һ����������â��������Ϊ10Ԫ/ǧ�ˣ��ۼ۲�����15Ԫ/ǧ�ˣ��Ҳ�����40Ԫ/ÿǧ�ˣ�����������������ָ�â����һ���ڵ�������![]() ��ǧ�ˣ��������ۼ�
��ǧ�ˣ��������ۼ�![]() ��Ԫ/ǧ�ˣ�֮��������������±���ʾ��һ�κ�����ϵ��
��Ԫ/ǧ�ˣ�֮��������������±���ʾ��һ�κ�����ϵ��
������ | �� | 32.5 | 35 | 35.5 | 38 | �� |
�ۼ� | �� | 27.5 | 25 | 24.5 | 22 | �� |
��1��ij������â���ۼ�Ϊ28Ԫ/ǧ�ˣ������â����������
��2����ij����������â������![]() Ԫ��д��
Ԫ��д��![]() ���ۼ�
���ۼ�![]() ֮��ĺ�����ϵʽ�����ˮ����������400Ԫ����ô����â�����ۼ�Ϊ����Ԫ��
֮��ĺ�����ϵʽ�����ˮ����������400Ԫ����ô����â�����ۼ�Ϊ����Ԫ��
����Ŀ����ˮ����˾������ˮɽ����ũ����Ʒ���������г���������.��������ʻʱ��ΪtСʱ��ƽ���ٶ�Ϊvǧ��/Сʱ��������ʻ�ٶȲ�����100ǧ��/Сʱ��.���ݾ��飬v,t��һ���Ӧֵ���±���
v(ǧ��/Сʱ) | 75 | 80 | 85 | 90 | 95 |
t(Сʱ) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
��1�����ݱ��е����ݣ����ƽ���ٶ�v��ǧ��/Сʱ��������ʻʱ��t(Сʱ)�ĺ�������ʽ��
��2����������7:30����ˮ�������ܷ�������10:00֮ǰ���ﺼ���У���˵�����ɣ�
��3�����������ﺼ���г�����ʻʱ��t����3.5��t��4����ƽ���ٶ�v��ȡֵ��Χ.