题目内容
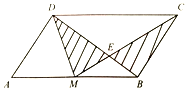
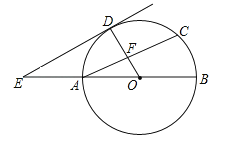
【题目】如图,AB为⊙O的直径,D为![]() 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)连接CD,若OA=AE=4,求四边形ACDE的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)欲证明DE是⊙O的切线,只要证明AC⊥OD,ED⊥OD即可.
(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD,推出S四边形ACDE=S△ODE,求出△ODE的面积即可.
(1)证明:∵D为![]() 的中点
的中点
∴OD⊥AC
∵AC∥DE
∴OD⊥DE
∴DE是⊙O的切线;
(2)解:连接DC,
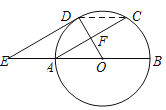
∵D为![]() 的中点
的中点
∴OD⊥AC,AF=CF
∵AC∥DE,且OA=AE
∴F为OD的中点,即OF=FD,在△AFO和△CFD中
∵AF=CF,∠AFO=∠CFD,OF=FD
∴△AFO≌△CFD(SAS)
∴S△AFO=S△CFD
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=4
∴OE=8
∴DE=![]() =
=![]()
∴S四边形ACDE=S△ODE=![]() ×OD×DE=
×OD×DE=![]() ×4×
×4×![]() =
=![]() .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目