题目内容
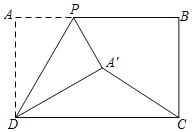
【题目】如图,点P为矩形ABCD的AB边上一动点,将△ADP沿着DP折叠,点A落在点A'处,连接CA',已知AB=10,AD=6,若以点P,B,C,A'为端点的线段(不再另外连接线段)构成的图形为直角三角形或特殊的平行四边形时,AP的长为 .
【答案】2或6.
【解析】
分两种情况讨论,由折叠的性质,矩形的性质和勾股定理可求解.
解:如图1,当点A'落在CD上,

∵将△ADP沿着DP折叠,点A落在点A'处,
∴AP=A'P,AD=A'D,∠DAP=∠DA'P=90°,
∴∠PA'C=90°,且∠B=∠C=90°,
∴四边形PBCA'是矩形,
∴BC=A'P=AP=6,
∴当AP=6时,四边形PBCA'是矩形,
如图2,当点P,点A',点C共线,

∵将△ADP沿着DP折叠,点A落在点A'处,
∴AP=A'P,AD=A'D=6,∠DAP=∠DA'P=90°,
∴A'C=![]() =
=![]() =8,
=8,
∴PC=8+A'P=8+AP,
∵PC2=PB2+BC2,
∴(8+AP)2=(10﹣AP)2+36,
∴AP=2,
故答案为:2或6.

练习册系列答案
相关题目