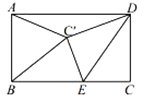
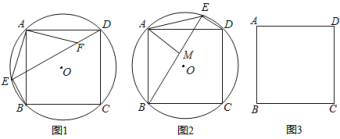
��Ŀ����
����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ��ɱ�Ϊ2Ԫ/ǧ�ˣ�ÿ��IJ���![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ����㺯����ϵʽ
��Ԫ/ǧ�ˣ����㺯����ϵʽ![]() �����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������
�����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
���ۼ۸� | 2 | 4 | ���� | 10 |
������� | 12 | 10 | ���� | 4 |
��֪����۲��Ź涨���ۼ۸�![]() ������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
��1��ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ����ע���Ա���
�ĺ�����ϵʽ����ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ��IJ���С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳�������ÿ��IJ��������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ�����
�ٵ�ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����ÿ���õ�����y����Ԫ�������ۼ۸�![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���ڣ�2���������£���![]() Ϊ______Ԫ/ǧ��ʱ������
Ϊ______Ԫ/ǧ��ʱ������![]() �����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���
�����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���![]() Ӧ��Ϊ______Ԫ/ǧ�ˣ�
Ӧ��Ϊ______Ԫ/ǧ�ˣ�
���𰸡���1��![]() ������
������![]() ����2��
����2��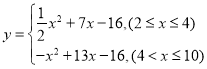 ����3��
����3��![]() ��5
��5
��������
(1)��![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() �����ݱ����е��������ô���ϵ����������⼴�ɣ�
�����ݱ����е��������ô���ϵ����������⼴�ɣ�
(2)����ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ���ݴ��в���ʽ������⼴�ɣ�
���ݴ��в���ʽ������⼴�ɣ�
�������Ա���Ϊ![]() ��
��![]() ��������ֱ���ʽ������⼴�ɣ�
��������ֱ���ʽ������⼴�ɣ�
(3)����(2)�е�������ö��κ��������ʷֱ�������ۼ�����ô�.
(1)�ɱ�������ݣ���![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ��
��
���ݱ�������ݵ�![]() �����
�����![]() ��
��
��![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ������
������![]() ��
��
(2)����ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ��
��
��![]() �����
�����![]() ��
��
��![]() �����Դ�ʱ
�����Դ�ʱ![]() ��
��
��������֪����![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��
ʱ��![]()
![]()
![]() ��
��
����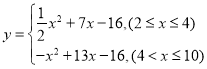 ��
��
(3)��![]() ʱ��
ʱ��
![]() �ĶԳ���Ϊ
�ĶԳ���Ϊ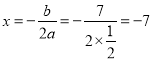 ��
��
����![]() ʱ��y����x�����������
ʱ��y����x�����������
��![]() ʱ�����ֵ��
ʱ�����ֵ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱȡ���ֵ��
ʱȡ���ֵ��
����ʱ![]() ���������
���������
Ҫʹÿ���������24��Ԫ����![]() ʱ����Ȼ�����ϣ�
ʱ����Ȼ�����ϣ�
��![]() �����
�����![]() ��
��
�ʵ�![]() ʱ���ܱ�֤������24��Ԫ��
ʱ���ܱ�֤������24��Ԫ��
�ʴ�Ϊ��![]() ��5.
��5.