Question

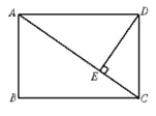
【题目】如图，在矩形ABCD中，DE⊥AC于E， ，AB＝3，

（1）求AD的值；

（2）直接写出的值是_____________.

Answer 1

【答案】（1） 4；（2）

【解析】（1）由四边形ABCD是矩形，易得AD=BC，∠ADE=∠BAC，结合AB=3，cos∠ADE=即可求得AC的长，再由勾股定理即可求得AD的长了；

（2）由（1）中所得AC、AD及CD的长结合S△ACD=AD·CD=AC·DE可求得DE的长，由此在△DEC中由勾股定理可得CE的长，这样就可求得△DEC的面积.

试题解析：

（1）∵四边形ABCD是矩形，DE⊥AC于点E，

∴AD=BC，CD=AB=3，∠BAD=∠ADC=∠AED=90°，

∴∠BAC+∠DAE=90°，∠DAE+∠ADE=90°，

∴∠BAC=∠ADE，

∵cos∠ADE=，

∴cos∠BAC=，即，解得：AC=5，

∴在Rt△ADC中，AD=；

（2）∵DE⊥AC于点E，

∴S△ADC=AC·DE=AD·DC，即DE=，解得DE=，

∴在Rt△DEC中，EC=，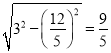

∴S△DEC=DE·EC=.