题目内容
【题目】已知如图所示，在Rt△ABC中，∠A＝90°，∠BCA＝75°，AC＝8cm，DE垂直平分BC，则BE的长是（ ）
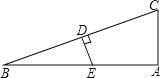
A.4cmB.8cmC.16cmD.32cm
【答案】C
【解析】
连接CE，先由三角形内角和定理求出∠B的度数，再由线段垂直平分线的性质及三角形外角的性质求出∠CEA的度数，由直角三角形中30°所对的直角边是斜边的一半即可解答．
解：连接CE，
∵Rt△ABC中，∠A＝90°，∠BCA＝75°，
∴∠B＝90°﹣∠BCA＝90°﹣75°＝15°，
∵DE垂直平分BC，
∴BE＝CE，
∴∠BCE＝∠B＝15°，
∴∠AEC＝∠BCE+∠B＝30°，
∵Rt△AEC中，AC＝8cm，
∴CE＝2AC＝16cm，
∵BE＝CE，
∴BE＝16cm．
故选：C．
练习册系列答案
相关题目
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销，经过调查，得到如下数据：
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
（1）研究发现，每天销售量
与单价
满足一次函数关系，求出与的关系式；
（2）当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润8000元？
