题目内容
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
【答案】D
【解析】试题解析:连接EO.
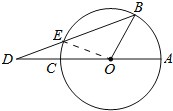
∵OB=OE,
∴∠B=∠OEB,
∵∠OEB=∠D+∠DOE,∠AOB=3∠D,
∴∠B+∠D=3∠D,
∴∠D+∠DOE+∠D=3∠D,
∴∠DOE=∠D,
∴ED=EO=OB,
故选D.
A、错误.假设DE=EB,则△EOB是等边三角形,则∠AOB=3∠D=90°,OB⊥AD,显然与题目不符.
B、错误.假设![]() DE=EB,则△EOB是等腰直角三角形,则∠AOB=3∠D=67.5°,显然与题目不符.
DE=EB,则△EOB是等腰直角三角形,则∠AOB=3∠D=67.5°,显然与题目不符.
C、错误.假设![]() DE=EB,则△EOB是等腰三角形,且底角∠B=30°,则∠AOB=45°,显然不符合题意.
DE=EB,则△EOB是等腰三角形,且底角∠B=30°,则∠AOB=45°,显然不符合题意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为弘扬中华传统文化,某校组织八年级![]() 名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为
名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为![]() 分)进行统计分析,得到如下所示的频数分布表:
分)进行统计分析,得到如下所示的频数分布表:
分数段 |
|
|
|
|
|
频数 |
|
|
|
|
|
所占百分比 |
|
|
|
|
|

请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为___ _,表中![]() _ ,
_ ,![]() _;
_;
(2)补全如图所示的频数分布直方图;
(3)若成绩超过![]() 分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?





