Question

【题目】若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：，.我们把它们称为根与系数关系定理.

如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为：AB=====

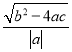
请你参考以上定理和结论，解答下列问题：

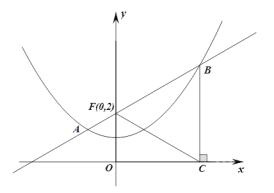
设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)，抛物线的顶点为C，显然△ABC为等腰三角形.

(1)当△ABC为等腰直角三角形时，直接写出b2-4ac的值；

(2)当△ABC为等腰三角形，且∠ACB=120°时，直接写出b2-4ac的值；

(3)设抛物线y=x2+mx+5与x轴的两个交点为A、B，顶点为C，且∠ACB=90°，试问如何平移此抛物线，才能使∠ACB=120°.

Answer 1

【答案】(1)4；(2)；(3)抛物线向上平移个单位后，向左或向右平移任意个单位都能使得度数由90°变为120°.

【解析】

（1）根据上述结论及直角三角形的性质列出等式，计算出即可；

（2）根据上述结论及含120°的等腰三角形的边角关系，列出方程，解出方程即可；

（3）根据（1）中结论，计算出m的值，设出平移后的函数解析式，根据（2）中结论，列出等量关系即可解出．

解：(1)由 y=ax2+bx+c(a≠0)可知顶点C

∵，

∴当△ABC为等腰直角三角形时，根据直角三角形斜边上的中线等于斜边的一半可知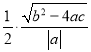：=，化简得

故答案为：4

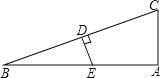
(2) 由 y=ax2+bx+c(a≠0)可知顶点C

如图，过点C作CD⊥AB交AB于点D，

∵∠ACB=120°，∴∠A=30°

∵tan30°= ，

即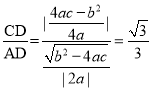，又因为，

∴化简得

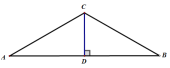
故答案为：

(3)∵

因为向左或向右平移时的度数不变,

所以只需将抛物线向上或向下平移使,然后向左或向右平移任意个单位即可.

设向上或向下平移后的抛物线的解析式为:,

平移后，

所以，抛物线向上平移个单位后，向左或向右平移任意个单位都能使得度数由变为.