Question

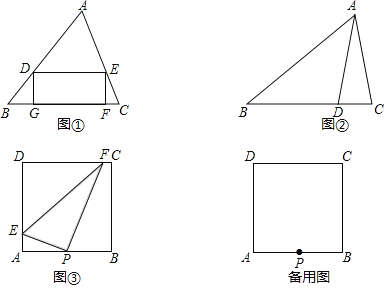
【题目】如图，在正方形ABCD中，等边△AEF的顶点E、F分别在BC和CD上．

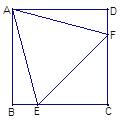
（1）、求证：△ABE≌△ADF；

（2）、若等边△AEF的周长为6，求正方形ABCD的边长．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题（1）根据四边形ABCD是正方形，得出AB=AD，∠B=∠D=90°，再根据△AEF是等边三角形，得出AE=AF，最后根据HL即可证出△ABE≌△ADF；

（2）根据等边△AEF的周长是6，得出AE=EF=AF的长，再根据（1）的证明得出CE=CF，∠C=90°，从而得出△ECF是等腰直角三角形，再根据勾股定理得出EC的值，设BE=x，则AB=x+，在Rt△ABE中，AB2+BE2=AE2，求出x的值，即可得出正方形ABCD的边长．

试题解析：（1）证明：∵四边形ABCD是正方形，

∴AB=AD，

∵△AEF是等边三角形，

∴AE=AF，

在Rt△ABE和Rt△ADF中，

∵AB＝AD，AE＝AF

∴Rt△ABE≌Rt△ADF；

（2）∵等边△AEF的周长是6，

∴AE=EF=AF=2，

又∵Rt△ABE≌Rt△ADF，

∴BE=DF，

∴CE=CF，∠C=90°，

即△ECF是等腰直角三角形，

由勾股定理得CE2+CF2=EF2，

∴EC=，

设BE=x，则AB=x+，

在Rt△ABE中，AB2+BE2=AE2，即（x+）2+x2=4，

解得x1=或x2=（舍去），

∴AB=+=，

∴正方形ABCD的边长为．

考点: 1.正方形的性质；2.全等三角形的判定与性质；