题目内容
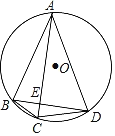
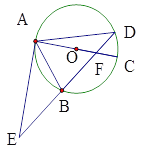
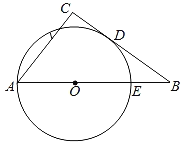
【题目】如图,BC是⊙O的切线,D是切点.连接BO并延长,交⊙O于点E、A,过A作AC⊥BC,垂足为C.若BD=8,BE=4,则AC=_____.
【答案】9.6
【解析】
连接OD、AD、ED,根据切线的性质得到∠ODB=90°,根据圆周角定理得到∠ADE=90°,证明△BDE∽△BAD,根据相似三角形的性质求出AE,证明△BDO∽△BCA,求出AC.
连接OD、AD、ED,
∵BC是⊙O的切线,
∴∠ODB=90°,
∴∠ODE+∠BDE=90°,
∵AE为⊙O的直径,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∵OD=OE
∴∠ODE=∠OED,
∴∠BDE=∠BAD,
∵∠B=∠B,
∴△BDE∽△BAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AE=12,
∵∠BDO=∠BCA,∠B=∠B,
∴△BDO∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=9.6,
故答案为:9.6.

练习册系列答案
相关题目