题目内容
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图像与性质,研究过程如下,请补充完整.
的图像与性质,研究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
| 10 |
| -2 | 1 |
| 1 | -2 | 3 | 10 |
|
其中,![]() _______,
_______,![]() =________;
=________;
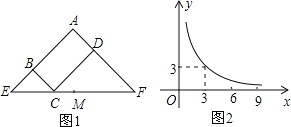
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图像;
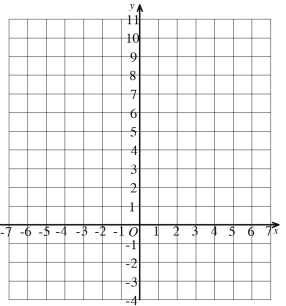
(3)观察函数图像:
①写出函数的一条图像性质:__________;
②当方程![]() 有且仅有两个不相等的实数根,根据函数图像直接写出
有且仅有两个不相等的实数根,根据函数图像直接写出![]() 的取值范围为________.
的取值范围为________.
【答案】(1)3;2;(2)图像见解析;①图像具有对称性,对称轴是直线![]() (或当
(或当![]() 或
或![]() 时,函数的最小值是-2,答案不唯一),②
时,函数的最小值是-2,答案不唯一),②![]() 或
或![]() .
.
【解析】
(1)将![]() ,
,![]() 代入函数解析式即可求出m,n的值;
代入函数解析式即可求出m,n的值;
(2)利用表格数据描点,再用平滑的曲线连接即可;
(3)①从图象与坐标轴的交点,图象的对称性,对称轴,增减性等方面写出一条性质即可;
②根据函数![]() 与
与![]() 有两个交点,结合图像即可得出答案.
有两个交点,结合图像即可得出答案.
(1)当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]()
∴![]()
故答案为:3,2;
(2)图像如下:
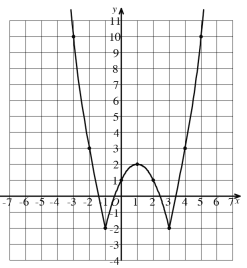
(3)①图像具有对称性,对称轴是直线![]() (或当
(或当![]() 或
或![]() 时,函数的最小值是-2,答案不唯一)
时,函数的最小值是-2,答案不唯一)
②方程![]() 可变形为
可变形为![]() ,
,
故找到函数![]() 与
与![]() 有两个交点的情况即可,
有两个交点的情况即可,
由图像可知,当![]() 或
或![]() 时,
时,
函数![]() 与
与![]() 有两个交点,
有两个交点,
故答案为:![]() 或
或![]()

【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?