题目内容
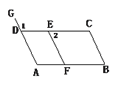
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
【答案】(1)AM=![]() DE,AM⊥DE,理由详见解析;(2)AM=
DE,AM⊥DE,理由详见解析;(2)AM=![]() DE,AM⊥DE,理由详见解析.
DE,AM⊥DE,理由详见解析.
【解析】
试题分析:(1)AM=![]() DE,AM⊥DE,理由是:先证明△DAE≌△BAG,得DE=BG,∠AED=∠AGB,再根据直角三角形斜边的中线的性质得AM=
DE,AM⊥DE,理由是:先证明△DAE≌△BAG,得DE=BG,∠AED=∠AGB,再根据直角三角形斜边的中线的性质得AM=![]() BG,AM=BM,则AM=
BG,AM=BM,则AM=![]() DE,由角的关系得∠MAB+∠AED=90°,所以∠AOE=90°,即AM⊥DE;(2)AM=
DE,由角的关系得∠MAB+∠AED=90°,所以∠AOE=90°,即AM⊥DE;(2)AM=![]() DE,AM⊥DE,理由是:作辅助线构建全等三角形,证明△MNG≌△MAB和△AGN≌△EAD可以得出结论.
DE,AM⊥DE,理由是:作辅助线构建全等三角形,证明△MNG≌△MAB和△AGN≌△EAD可以得出结论.
试题解析:(1)AM=![]() DE,AM⊥DE,理由是:
DE,AM⊥DE,理由是:
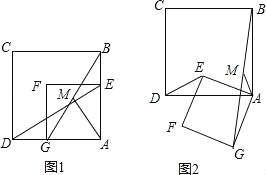
如图1,设AM交DE于点O,
∵四边形ABCD和四边形AEFG都是正方形,
∴AG=AE,AD=AB,
∵∠DAE=∠BAG,
∴△DAE≌△BAG,
∴DE=BG,∠AED=∠AGB,
在Rt△ABG中,
∵M为线段BG的中点,
∴AM=![]() BG,AM=BM,
BG,AM=BM,
∴AM=![]() DE,
DE,
∵AM=BM,
∴∠MBA=∠MAB,
∵∠AGB+∠MBA=90°,
∴∠MAB+∠AED=90°,
∴∠AOE=90°,即AM⊥DE;
(2)AM=![]() DE,AM⊥DE,理由是:
DE,AM⊥DE,理由是:
如图2,延长AM到N,使MN=AM,连接NG,
∵MN=AM,MG=BM,∠NMG=∠BMA,
∴△MNG≌△MAB,
∴NG=AB,∠N=∠BAN,
由(1)得:AB=AD,
∴NG=AD,
∵∠BAN+∠DAN=90°,
∴∠N+∠DAN=90°,
∴NG⊥AD,
∴∠AGN+∠DAG=90°,
∵∠DAG+∠DAE=∠EAG=90°,
∴∠AGN=∠DAE,
∵NG=AD,AG=AE,
∴△AGN≌△EAD,
∴AN=DE,∠N=∠ADE,
∵∠N+∠DAN=90°,
∴∠ADE+∠DAN=90°,
∴AM⊥DE.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案