题目内容
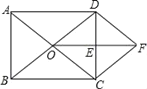
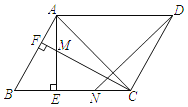
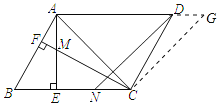
【题目】如图,在ABCD中,∠ACB=45°,AE⊥BC于点E,过点C作CF⊥AB于点F,交AE于点M.点N在边BC上,且AM=CN,连结DN.
(1)若AB=![]() ,AC=4,求BC的长;
,AC=4,求BC的长;
(2)求证:AD+AM=![]() DN.
DN.
【答案】(1)3![]() ;(2)见解析
;(2)见解析
【解析】
(1)证出△ACE是等腰直角三角形,由勾股定理得:AE=CE=2![]() ,BE=
,BE=![]() =
=![]() ,即可得出结果;
,即可得出结果;
(2)延长AD至G,使DG=AM,证出四边形CGDN是平行四边形,得出CG=DN,证明△ABE≌△CME,得出AB=CM,∠B=∠CME,再证明△ACM≌△GCD,得出∠G=∠MAC=45°,证出△ACG是等腰直角三角形,得出AG=![]() CG,即可得出结论.
CG,即可得出结论.
(1)解:∵∠ACB=45°,AE⊥BC,
∴∠AEC=∠AEB=90°,△ACE是等腰直角三角形,
∴∠EAC=45°,AE=CE=![]() =
=![]() =2
=2![]() ,
,
由勾股定理得:BE=![]() =
=![]() =
=![]() ,
,
∴BC=BE+CE=3![]() ;
;
(2)证明:延长AD至G,使DG=AM,连接CG,如图所示:
∵AM=CN,
∴DG=CN,
∵四边形ABCD是平行四边形,
∴AB=CD,AD//BC,∠B=∠ADC,
∴DG∥CN,
∴四边形CGDN是平行四边形,
∴CG=DN,
∵CF⊥AB,
∴∠CFB=90°=∠AEB=∠CEA,
∴∠BAE=∠MCE,
在△ABE和△CME中,
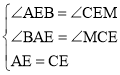 ,
,
∴△ABE≌△CME(AAS),
∴AB=CM,∠B=∠CME,
∴CM=CD,∠CME=∠ADC,
∴∠AMC=∠GDC,
在△ACM和△GCD中,
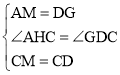 ,
,
∴△ACM≌△GCD(SAS),
∴∠G=∠MAC=45°,
∵AD//BC,
∴∠DAC=∠ACB=45°,
∴△ACG是等腰直角三角形,
∴AG=![]() CG,
CG,
∵AG=AD+DG=AD+AM,CG=DN,
∴AD+AM=![]() DN.
DN.

【题目】已知![]() 是
是![]() 的反比例函数,下表给出了
的反比例函数,下表给出了![]() 与
与![]() 的一些值.
的一些值.
| … | -4 | -2 | -1 | 1 | 3 | 4 | … | ||
| … | -2 | 6 | 3 | … |
(1)求出这个反比例函数的表达式;
(2)根据函数表达式完成上表;
(3)根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.