Question

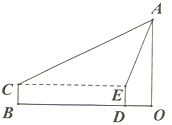
【题目】某中学为数学实验“先行示范校”，一数学活动小组带上高度为1.5m的测角仪BC，对建筑物AO进行测量高度的综合实践活动，如图，在BC处测得直立于地面的AO顶点A的仰角为30°，然后前进40m至DE处，测得顶点A的仰角为75°.

（1）求∠CAE的度数；

（2）求AE的长（结果保留根号）；

（3）求建筑物AO的高度（精确到个位，参考数据：,）.

Answer 1

【答案】（1）45°；（2）；（3）29.

【解析】

（1）先根据测得顶点A的仰角为75°，求出∠AEC的度数进而求∠CAE的度数；

（2）延长CE交AO于点G，过点E作EF⊥AC垂足为F．解直角三角形即可得到结论；

（3）根据题干条件直接解直角三角形即可得到结论．

解：（1）由测得顶点A的仰角为75°，可知∠AEC=180°-75°=105°，又顶点A的仰角为30°即∠ACE=30°，所以∠CAE=180°-105°-30°=45°；

（2）延长CE交AO于点G，过点E作EF⊥AC垂足为F．

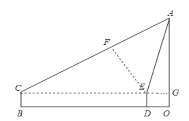
由题意可知：∠ACG=30°，∠AEG=75°，CE=40，

∴∠EAC=∠AEG-∠ACG=45°，

∵EF=CE×Sin∠FCE=20，

∴AE=，

∴AE的长度为m；；

（3）∵CF=CE×cos∠FCE=，AF=EF=20，

∴AC=CF+AF=+20，

∴AG=AC×Sin∠ACG=，

∴AO=AG+GO=+1.5=≈29，

∴高度AO约为29m．