题目内容
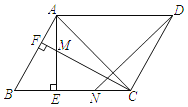
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A，B的距离，他们设计了如图的测量方案：从树A沿着垂直于AB的方向走到E，再从E沿着垂直于AE的方向走到F，C为AE上一点，其中4位同学分别测得四组数据：①AC，∠ACB；②EF，DE，AD；③CD，∠ACB，∠ADB；④∠F，∠ADB，FB．其中能根据所测数据求得A，B两树距离的有（ ）
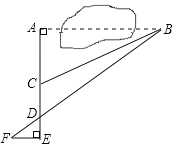
A.1组B.2组C.3组D.4组
【答案】C
【解析】
根据三角函数的定义及相似三角形的判定定理及性质对各选项逐一判断即可得答案．
∵已知∠ACB的度数和AC的长，
∴利用∠ACB的正切可求出AB的长，故①能求得A，B两树距离，
∵AB//EF，
∴△ADB∽△EDF，
∴
，故②能求得A，B两树距离，
设AC＝x，
∴AD＝CD+x，AB＝
，AB＝
；
∵已知CD，∠ACB，∠ADB，
∴可求出x，然后可得出AB，故③能求得A，B两树距离，
已知∠F，∠ADB，FB不能求得A，B两树距离，故④求得A，B两树距离，
综上所述：求得A，B两树距离的有①②③，共3个，
故选：C．
练习册系列答案
相关题目
