题目内容
【题目】问题探究:
(1)如图①所示是一个半径为![]() ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形
,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形![]() 则蚂蚁爬行的最短路程即为线段
则蚂蚁爬行的最短路程即为线段![]() 的长)
的长)
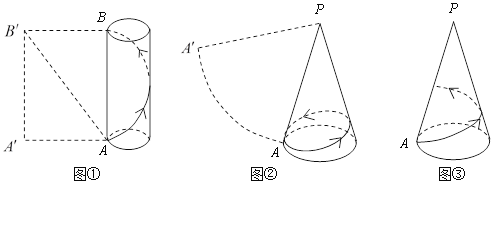
(2)如图②所示是一个底面半径为![]() ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
【答案】(1)蚂蚁爬行的最短路程为5; (2)最短路程为![]() ;(3)蚂蚁爬行的最短距离为
;(3)蚂蚁爬行的最短距离为![]()
【解析】
(1)蚂蚁爬行的最短路程为圆柱侧面展开图即矩形的对角线的长度,由勾股定理可求得;
(2)蚂蚁爬行的最短路程为圆锥展开图中的AA′的连线,可求得△PAA′是等边三角形,则AA′=PA=4;
(3)蚂蚁爬行的最短路程为圆锥展开图中点A到PA的距离.
(1)由题意可知:
![]()
在![]() 中,
中,![]()
即蚂蚁爬行的最短路程为5.
(2)连结![]() 则
则![]() 的长为蚂蚁爬行的最短路程,设
的长为蚂蚁爬行的最短路程,设![]() 为圆锥底面半径,
为圆锥底面半径,![]() 为侧面展开图(扇形)的半径,
为侧面展开图(扇形)的半径,
则![]() 由题意得:
由题意得:![]()
即![]()
![]()
![]() 是等边三角形
是等边三角形
![]() 最短路程为
最短路程为![]()
(3)如图③所示是圆锥的侧面展开图,过![]() 作
作![]() 于点
于点![]() 则线段
则线段![]() 的长就是蚂蚁爬行的最短路程.
的长就是蚂蚁爬行的最短路程.
在Rt△ACP中,
∵∠P=60°,
∴∠PAC=30°
∴PC=![]() PA=
PA=![]() ×4=2
×4=2
∴AC=![]() =
=![]()
![]() 蚂蚁爬行的最短距离为
蚂蚁爬行的最短距离为![]()


练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目