Question

【题目】如图1，在中，为锐角．点为射线上一动点，连接，以为一边且在的右侧作正方形．

解答下列问题：

如果，．

①当点在线段上时（与点不重合），如图2，线段、之间的位置关系为________，数量关系为________．

②当点在线段的延长线上时，如图3，①中的结论是否仍然成立，为什么？

如果，，点在线段上运动．试探究：当满足一个什么条件时，（点、重合除外）？画出相应图形，并说明理由．（画图不写作法）

Answer 1

【答案】（1）垂直，相等； 当时，，理由见解析.

【解析】

（1）①根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB≌△FAC，根据全等三角形的性质即可得到结论；②由正方形ADEF的性质可推出△DAB≌△FAC，根据全等三角形的性质得到CF=BD，∠ACF=∠ABD，根据余角的性质即可得到结论；

（2）过点A作AG⊥AC交CB或CB的延长线于点G，于是得到∠GAC=90°，可推出∠ACB=∠AGC，证得AC=AG，根据（1）的结论于是得到结果．

（1）①正方形ADEF中，AD=AF．

∵∠BAC=∠DAF=90°，∴∠BAD=∠CAF．在△DAB与△FAC中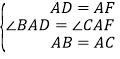，，∴△DAB≌△FAC，∴CF=BD，∠B=∠ACF，∴∠ACB+∠ACF=90°，即CF⊥BD．

故答案为：垂直、相等；

②成立，理由如下：

∵∠FAD=∠BAC=90°

∴∠BAD=∠CAF

在△BAD与△CAF中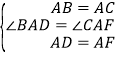，∵，∴△BAD≌△CAF，∴CF=BD，∠ACF=∠ACB=45°，∴∠BCF=90°，∴CF⊥BD；

（2）当∠ACB=45°时，CF⊥BD（如图）．

理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC=90°．

∵∠ACB=45°，∠AGC=90°﹣∠ACB，∴∠AGC=90°﹣45°=45°，∴∠ACB=∠AGC=45°，∴AC=AG．在△GAD与△CAF中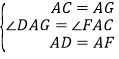，，∴△GAD≌△CAF，∴∠ACF=∠AGC=45°，∠BCF=∠ACB+∠ACF=45°+45°=90°，即CF⊥BC．