题目内容
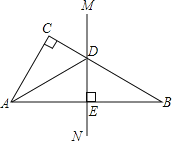
【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BOE=75°.
【解析】分析:(1)由矩形的性质和角平分线的性质得出△ABE是等腰直角三角形;
(2)由矩形的性质得出OA=OB,再由角的和差关系可得∠AOB=60°,即可得出结论;
(3)由(2)的结论得出∠OBE=30°,证出OB=BE,求出∠BOE的度数即可.
详解:(1)∵四边形ABCD是矩形,∴∠BAD=∠ABE=90°.
∵AE平分∠BAD,∴∠BAE=45°,∴△ABE是等腰直角三角形;
(2)∵四边形ABCD是矩形,∴OA=OB.
∵∠CAE=15°,∴∠BAO=45°+15°=60°,∴△AOB是等边三角形;
(3)由(2)得:△AOB是等边三角形,∴∠ABO=60°,∴∠OBE=90°﹣60°=30°.
∵BE=AB,OB=AB,∴OB=BE,∴∠BOE=![]() (180°﹣30°)=75°.
(180°﹣30°)=75°.

练习册系列答案
相关题目