题目内容
【题目】如图，在平面直角坐标系中，点A、B均在函数y= 
（k＞0，x＞0）的图象上，⊙A与x轴相切，⊙B与y轴相切．若点B的坐标为（1，6），⊙A的半径是⊙B的半径的2倍，则点A的坐标为（ ） 
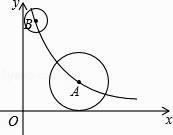
A.（2，2）
B.（2，3）
C.（3，2）
D.（4， 
）
【答案】C
【解析】解：把B的坐标为（1，6）代入反比例函数解析式得：k=6， 则函数的解析式是：y= 
，
∵B的坐标为（1，6），⊙B与y轴相切，
∴⊙B的半径是1，
则⊙A是2，
把y=2代入y= 得：x=3，
则A的坐标是（3，2）．
故选：C．
【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．
阅读快车系列答案
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”，下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
（1）仔细观察，表一中a为大于1的奇数，此时b、c的数量关系是_____________，
a、b、c之间的数量关系是_________________________；
（2）仔细观察，表二中a为大于4的偶数，此时b、c的数量关系是_____________，
a、b、c之间的数量关系是_________________________；
（3）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，12，13”与表二中的“10，24，26”恰好也成倍数关系……请直接利用这一规律计算：在Rt△ABC中，当
，
时，斜边c的值.
