Question

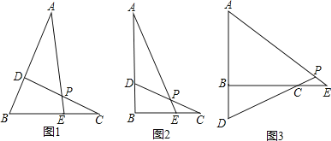
【题目】如图，已知，⊙O的半径，弦AB，CD交于点E，C为的中点，过D点的直线交AB延长线与点F，且DF=EF．

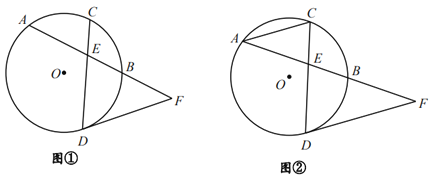
（1）如图①，试判断DF与⊙O的位置关系，并说明理由；

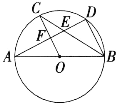
（2）如图②，连接AC，若AC∥DF，BE=AE，求CE的长．

Answer 1

【答案】（1）DF与⊙O相切，理由见解析；（2）CE=2．

【解析】

（1）如图，作辅助线；证明∠ODC+∠CDF=90°，即可解决问题．

（2）如图，作辅助线；证明OH⊥AB，AH=4λ，此为解题的关键性结论；证明CE=λ；列出方程r2=（r-3λ）2+（4λ）2，求出λ=r=×=2，即可解决问题．

（1）DF与⊙O相切．

如图1，连接OC、OD；

∵C为弧AB的中点，

∴OC⊥AB，∠OCE+∠AEC=90°；

∴DF=EF，

∴∠FDE=∠FED=∠AEC；

∵OA=OC，

∴∠OCE=∠ODC，

∴∠ODC+∠CDF=90°，

即OD⊥DF，

∴DF与⊙O相切．

（2）如图2，连接OA、OC；

由（1）知OC⊥AB，

∴AH=BH；

∵AC∥DF，

∴∠ACD=∠CDF；而EF=DF，

∴∠DEF=∠CDF=∠ACD，

∴AC=AE；

设AE=5λ，则BE=3λ，

∴AH=4λ，HE=λ，AC=AE=5λ；

∴由勾股定理得：CH=3λ；

CE2=CH2+HE2=9λ2+λ2，

∴CE=λ；

在直角△AOH中，由勾股定理得：

AO2=AH2+OH2，

即r2=（r-3λ）2+（4λ）2，

解得：λ=r=×=2，

∴CE=2．