题目内容
【题目】已知：点A、C分别是∠B的两条边上的点，点D、E分别是直线BA、BC上的点，直线AE、CD相交于点P．
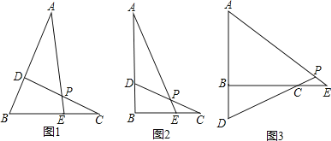
（1）点D、E分别在线段BA、BC上；
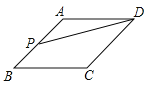
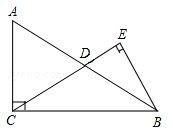
①若∠B＝60°（如图1），且AD＝BE，BD＝CE，则∠APD的度数为 ；
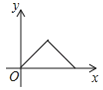
②若∠B＝90°（如图2），且AD＝BC，BD＝CE，求∠APD的度数；
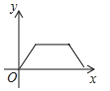
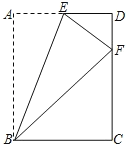
（2）如图3，点D、E分别在线段AB、BC的延长线上，若∠B＝90°，AD＝BC，∠APD＝45°，求证：BD＝CE．
【答案】（1）①60°；②45°；（2）见解析
【解析】
（1）连结AC，由条件可以得出△ABC为等边三角形，再由证△CBD≌△ACE就可以得出∠BCD=∠CAE，就可以得出结论；
（2）作AF⊥AB于A，使AF=BD，连结DF，CF，就可以得出△FAD≌△DBC，再证△DCF为等腰直角三角形，由∠FAD=∠B=90°，就可以得出AF∥BC，就可以得出四边形AECF是平行四边形，就有AE∥CF，就可以得出∠EAC=∠FCA，就可以得出结论；
（3）作AF⊥AB于A，使AF=BD，连结DF，CF，就可以得出△FAD≌△DBC，再证△DCF为等腰直角三角形，就有∠DCF=∠APD=45°，推出CF∥AE，由∠FAD=∠B=90°，就可以得出AF∥BC，就可以得出四边形AFCE是平行四边形，就有AF=CE．
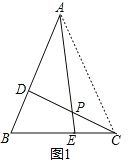
（1）①如图1，连结AC，
∵AD＝BE，BD＝CE，
∴AD+BD＝BE+CE，
∴AB＝BC．
∵∠B＝60°，
∴△ABC为等边三角形．
∴∠B＝∠ACB＝60°，BC＝AC．
在△CBD和△ACE中
，
∴△CBD≌△ACE（SAS），
∴∠BCD＝∠CAE．
∵∠APD＝∠CAE+∠ACD，
∴∠APD＝∠BCD+∠ACD＝60°．
故答案为60°；
②如图2，作AF⊥AB于A，使AF＝BD，连结DF，CF，
∴∠FAD＝90°．
∵∠B＝90°，
∴∠FAD＝∠B．
在△FAD和△DBC中，
，
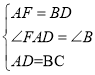∴△FAD≌△DBC（SAS），
∴DF＝DC，∠ADF＝∠BCD．
∵∠BDC+∠BCD＝90°，
∴∠ADF+∠BDC＝90°，
∴∠FDC＝90°，
∴∠FCD＝45°．
∵∠FAD＝90°，∠B＝90，
∴∠FAD+∠B＝180°，
∴AF∥BC．
∵DB＝CE，
∴AF＝CE，
∴四边形AECF是平行四边形，
∴AE∥CF，
∴∠EAC＝∠FCA．
∵∠APD＝∠ACP+∠EAC，
∴∠APD＝∠ACP+∠ACE＝45°；
（2）如图3，作AF⊥AB于A，使AF＝BD，连结DF，CF，
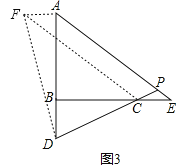
∴∠FAD＝90°．
∵∠ABC＝90°，
∴∠FAD＝∠DBC＝90°．
在△FAD和△DBC中，
，
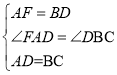∴△FAD≌△DBC（SAS），
∴DF＝DC，∠ADF＝∠BCD．
∵∠BDC+∠BCD＝90°，
∴∠ADF+∠BDC＝90°，
∴∠FDC＝90°，
∴∠FCD＝45°．
∵∠APD＝45°，
∴∠FCD＝∠APD，
∴CF∥AE．
∵∠FAD＝90°，∠ABC＝90，
∴∠FAD＝∠ABC，
∴AF∥BC．
∴四边形AECF是平行四边形，
∴AF＝CE，
∴CE＝BD．
