题目内容
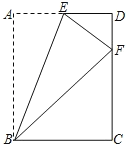
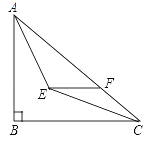
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC与∠ACB的平分线相较于点E,过点E作EF∥BC交AC于点F,则EF的长为________.
【答案】![]()
【解析】
延长FE交AB于点D,作EG⊥BC、作EH⊥AC,由EF∥BC可证四边形BDEG是矩形,由角平分线可得ED=EH=EG、∠DAE=∠HAE,从而知四边形BDEG是正方形,再证△DAE≌△HAE、△CGE≌△CHE得AD=AH、CG=CH,设BD=BG=x,则AD=AH=6-x、CG=CH=8-x,由AC=10可得x=2,即BD=DE=2、AD=4,再证△ADF∽△ABC可得DF=![]() ,据此得出EF=DF-DE=
,据此得出EF=DF-DE=![]() .
.
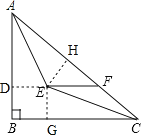
如图,延长FE交AB于点D,作EG⊥BC于点G,作EH⊥AC于点H,
∵EF∥BC、∠ABC=90°,
∴FD⊥AB,
∵EG⊥BC,
∴四边形BDEG是矩形,
∵AE平分∠BAC、CE平分∠ACB,
∴ED=EH=EG,∠DAE=∠HAE,
∴四边形BDEG是正方形,
在△DAE和△HAE中,
∵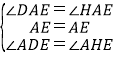 ,
,
∴△DAE≌△HAE(SAS),
∴AD=AH,
同理△CGE≌△CHE,
∴CG=CH,
设BD=BG=x,则AD=AH=6-x、CG=CH=8-x,
∵AC=![]() =10,
=10,
∴6-x+8-x=10,
解得:x=2,
∴BD=DE=2,AD=4,
∵DF∥BC,
∴△ADF∽△ABC,
∴![]() ,即
,即![]() ,
,
解得:DF=![]() ,
,
则EF=DF-DE=![]() -2=
-2=![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目