题目内容
【题目】如图,已知二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
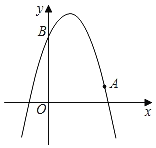
(1)求该二次函数的表达式及顶点坐标;
(2)点C(m,n)在该二次函数图象上.
①当m=﹣1时,求n的值;
②当m≤x≤3时,n最大值为5,最小值为1,请根据图象直接写出m的取值范围.
【答案】(1)y=﹣(x﹣1)2+5,顶点为(1,5);(2)①n=1;②﹣1≤m≤1
【解析】
(1)根据待定系数法即可求得;
(2)①把x=﹣1代入(1)中求得的解析式求得函数y的值,即可求得n的值;
②把y=1代入抛物线解析式求得对应的x的值,然后根据图象即可求得m的取值范围.
解:(1)∵二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
∴![]() ,解得
,解得![]() ,
,
∴该二次函数为y=﹣x2+2x+4,
∵y=﹣(x﹣1)2+5,
∴顶点为(1,5);
(2)∵点C(m,n)在该二次函数图象上,
①当m=﹣1时,则C(﹣1,n),
把C(﹣1,n)代入y=﹣x2+2x+4得,
n=-1-2+4=1,
∴n=1;
②∵y=﹣(x﹣1)2+5,
∴当x=3时,y=﹣(3﹣1)2+5=1,抛物线对称轴是直线x=1,函数的最大值是5,
∴点(3,1)关于关于对称轴的对称点是(-1,1),抛物线的顶点为(1,5).
∵当m≤x≤3时,n最大值为5,最小值为1,
∴m的取值范围是-1≤m≤1.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
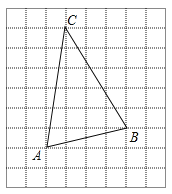
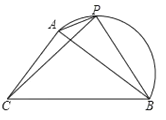
同步奥数系列答案【题目】如图,在△ABC中,AB=4cm.BC=5cm,P是![]() 上的动点.设A,P两点间的距离为xcm,
上的动点.设A,P两点间的距离为xcm,
B,P两点间的距离为![]() cm,C,P两点间的距离为
cm,C,P两点间的距离为![]() cm.
cm.
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 |
| 4.00 | 3.69 | 2.13 | 0 | |
| 3.00 | 3.91 | 4.71 | 5.23 | 5 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象:
的图象:
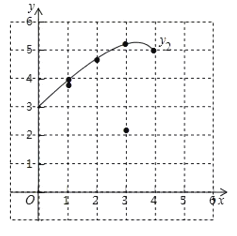
(3)结合函数图象.
①当△PBC为等腰三角形时,AP的长度约为____cm.
②记![]() 所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.
所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.