题目内容
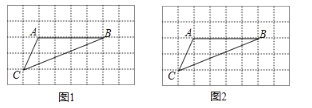
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均落在格点上,
均落在格点上,
(1)![]() 的长等于________;
的长等于________;
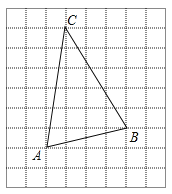
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
【答案】(1)![]() ;(2)答案见解析
;(2)答案见解析
【解析】
(1)利用勾股定理即可解决问题;
(2)如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求.
解:(1)![]()
故答案为:![]() ;
;
(2)如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求.
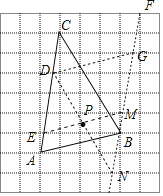
理由:平行四边形ABME的面积:平行四边形CDNB的面积:平行四边形DEMG的面积=1:2:3,
△PAB的面积=![]() 平行四边形ABME的面积,△PBC的面积=
平行四边形ABME的面积,△PBC的面积=![]() 平行四边形CDNB的面积,△PAC的面积=△PNG的面积=
平行四边形CDNB的面积,△PAC的面积=△PNG的面积=![]() △DGN的面积=
△DGN的面积=![]() 平行四边形DEMG的面积,
平行四边形DEMG的面积,
∴S△PAB:S△PBC:S△PCA=1:2:3.

练习册系列答案
相关题目