Question

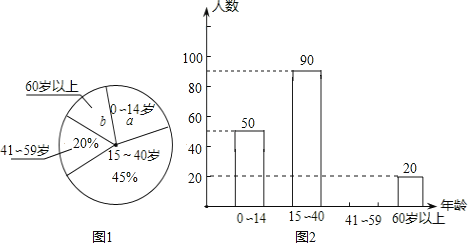
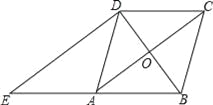
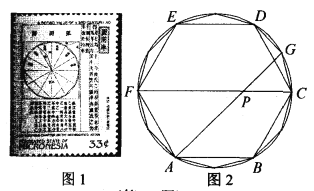
【题目】我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出，“周三径一”不是圆周率值，实际上是圆内接正六边形周长和直径的比值（图1）．刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法．如图2，六边形是圆内接正六边形，把每段弧二等分，作出一个圆内接正十二边形，连结交于点若，则的长为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

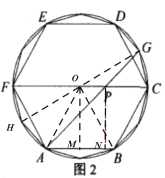
过点P作PN⊥AB，连接HG交FC于点O，连接OA，OB，过点O⊥与AB于M，可知∠PAB=45°，可求OM=PN=，再解Rt△AMO，求得圆的半径长，进而可求圆周长，再根据=圆周长÷12求得CG的长即可．

解：如图，过点P作PN⊥AB，连接HG交FC于点O，连接OA，OB，过点O⊥与AB于M，

∴∠PAB=45°，

∴PN=OM=，

∵OA=OB，∠AOB=60°，

∴∠AOM=30°，

∴，

即圆的半径为4，

∴圆的周长为：，

∴，

故选：D．