题目内容
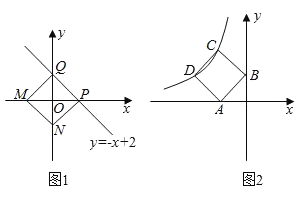
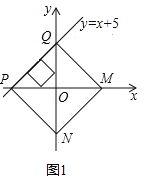
【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
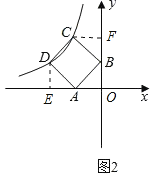
(2)若某函数是反比例函数y=![]() (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
【答案】(1)一次函数y=x+5图象的“梦幻正方形”的边长为5![]() 或
或![]() ;(2)m=2.反比例函数的解析式为y=﹣
;(2)m=2.反比例函数的解析式为y=﹣![]()
【解析】
(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长;
(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点![]() 的坐标表示出点C的坐标,再利用待定系数法得到一个关于m、k方程组,然后求解即可.
的坐标表示出点C的坐标,再利用待定系数法得到一个关于m、k方程组,然后求解即可.
(1)如图1,当点M在x轴正半轴,点N在y轴负半轴上时
![]()
∴正方形MNPQ的边长![]()
设小正方形的边长为a
则![]()
解得![]() ,即小正方形边长为
,即小正方形边长为![]()
故一次函数![]() 图象的“梦幻正方形”的边长为
图象的“梦幻正方形”的边长为![]() 或
或![]() ;
;
(2)如图2,作DE,CF分别垂直于x、y轴
易知![]()
![]()
![]()
![]()
![]()
∴C点坐标为![]()
将点C、D坐标代入反比例函数的解析式得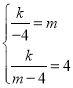
解得![]()
故反比例函数的解析式为![]() .
.

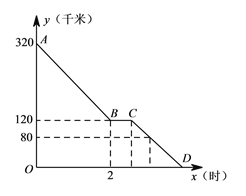
【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
该商品在销售过程中,销售量![]() (件)与
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
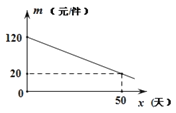
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?