ЬтФПФкШн
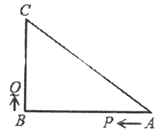
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯB=90ЁуЃЌAB=8cmЃЌBC=6cmЃЌPЁЂQЪЧЁїABCБпЩЯЕФСНИіЖЏЕуЃЌЦфжаPЕуДгЕуAПЊЪМбиABЗНЯђдЫЖЏЧвЫйЖШЮЊУПУыlcmЃЌЕуQДгЕуBПЊЪМбиBЁњCЁњAЗНЯђдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌЫќУЧЭЌЪБГіЗЂЃЌЩшГіЗЂЕФЪБМфЮЊtУы.
(1)ГіЗЂ2УыКѓЃЌЧѓЯпЖЮPQЕФГЄ?
(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂЖљУыжгКѓЃЌOPQBЪЧЕШбќШ§НЧаЮ?
(3)ЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌЧѓФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМф?
ЁОД№АИЁП(1)ГіЗЂ2УыКѓЃЌЯпЖЮPQЕФГЄЮЊ![]() ЃЛ(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ
ЃЛ(2)ЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ![]() УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ (3)ЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.
УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ (3)ЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуPЁЂQЕФдЫЖЏЫйЖШЧѓГіAPЃЌдйЧѓГіBPКЭBQЃЌгУЙДЙЩЖЈРэЧѓЕУPQМДПЩЃЛ
ЃЈ2ЃЉЩшГіЗЂtУыжгКѓЃЌЁїPQBФмаЮГЩЕШбќШ§НЧаЮЃЌдђBP=BQЃЌгЩBQ=2tЃЌBP=8-tЃЌСаЪНЧѓЕУtМДПЩЃЛ
ЃЈ3ЃЉЕБЕуQдкБпCAЩЯдЫЖЏЪБЃЌФмЪЙЁїBCQГЩЮЊЕШбќШ§НЧаЮЕФдЫЖЏЪБМфгаШ§жжЧщПіЃКЂйЕБCQ=BQЪБЃЈЭМ1ЃЉЃЌдђЁЯC=ЁЯCBQЃЌПЩжЄУїЁЯA=ЁЯABQЃЌдђBQ=AQЃЌдђCQ=AQЃЌДгЖјЧѓЕУtЃЛ
ЂкЕБCQ=BCЪБЃЈШчЭМ2ЃЉЃЌдђBC+CQ=12ЃЌвзЧѓЕУtЃЛ
ЂлЕБBC=BQЪБЃЈШчЭМ3ЃЉЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌдђЧѓГіBEЃЌCEЃЌМДПЩЕУГіtЃЎ
(1)BQ=2ЁС2=4cmЃЌBP=ABAP=82ЁС1=6cmЃЌ
ЁпЁЯB=90ЁуЃЌ
гЩЙДЙЩЖЈРэЕУЃКPQ=![]() ,
,
ЁрГіЗЂ2УыКѓЃЌЯпЖЮPQЕФГЄЮЊ![]() ЃЛ
ЃЛ
(2)BQ=2tЃЌBP=8-t ЃЌ
гЩЬтвтЕУЃК2t=8-t ЃЌ
НтЕУЃКt=![]() ЃЌ
ЃЌ
ЁрЕБЕуQдкБпBCЩЯдЫЖЏЪБЃЌГіЗЂ![]() УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ
УыКѓЃЌЁїPQBЪЧЕШбќШ§НЧаЮЃЛ
(3) ЁпЁЯABC=90ЁуЃЌBC=6ЃЌAB=8ЃЌ
ЁрAC=![]() =10.
=10.
ЂйЕБCQ=BQЪБ(ЭМ1)ЃЌдђЁЯC=ЁЯCBQЃЌ
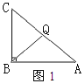
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯCBQ+ЁЯABQ=90ЁуЃЌЁЯA+ЁЯC=90ЁуЃЌ
ЁрЁЯA=ЁЯABQЃЌ
ЁрBQ=AQЃЌ
ЁрCQ=AQ=5ЃЌ
ЁрBC+CQ=11ЃЌ
Ёрt=11ЁТ2=5.5УыЃЛ
ЂкЕБCQ=BCЪБ(ШчЭМ2)ЃЌ
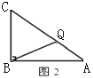
дђBC+CQ=12ЃЌ
Ёрt=12ЁТ2=6УыЃЌ
ЂлЕБBC=BQЪБ(ШчЭМ3)ЃЌЙ§BЕузїBEЁЭACгкЕуEЃЌ
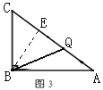
ЁрBE=![]() ЃЌ
ЃЌ
ЫљвдCE=![]() =
=![]() =3.6ЃЌ
=3.6ЃЌ
ЙЪCQ=2CE=7.2ЃЌ
ЫљвдBC+CQ=13.2ЃЌ
Ёрt=13.2ЁТ2=6.6Уы.
гЩЩЯПЩжЊЃЌЕБtЮЊ5.5УыЛђ6УыЛђ6.6УыЪБЃЌЁїBCQЮЊЕШбќШ§НЧаЮ.

 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ