题目内容
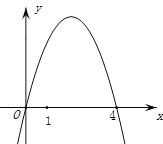
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0在1<x<5的范围内有解,则t的取值范围是( )
A. t>-5 B. -5<t<3 C. -5<t≤4 D. 3<t≤4
【答案】C
【解析】分析:由对称轴为x=2,求出m的值,根据在1<x<5的范围内抛物线y=-x2+4x与直线y=t有交点求t的范围.
详解:因为![]() ,所以m=4,则一元二次方程为-x2+4x-t=0.
,所以m=4,则一元二次方程为-x2+4x-t=0.
即在1<x<5的范围内抛物线y=-x2+4x与直线y=t有交点.
①当x=2时,y=-22+2×4=4,所以t≤4;
②当x=5时,y=-52+5×4=-5,所以t>-5;
∴-5<x≤4.
所以t的范围是-5<t≤4.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目