题目内容
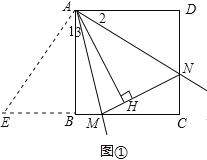
【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
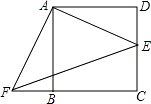
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

【答案】(1)AB=AH,理由见解析;(2)6
【解析】(1)延长CB至E使BE=DN,连接AE,由三角形全等可以证明AB=AH;
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,延长EB、FC交于点G,则四边形AEGF是矩形,又![]() ,所以四边形AEGF是正方形,设AD=x,则EG=AE=AD=FG=x,则BG=x2;CG=x3;BC=2+3=5,在Rt△BGC中,
,所以四边形AEGF是正方形,设AD=x,则EG=AE=AD=FG=x,则BG=x2;CG=x3;BC=2+3=5,在Rt△BGC中,![]() 解之得
解之得![]() 所以AD的长为6.
所以AD的长为6.
(1)答:AB=AH,
证明:延长CB至E使BE=DN,连接AE,
∵四边形ABCD是正方形,
∴![]()
∴![]()
又∵AB=AD,
∵在△ABE和△ADN中,
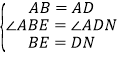 ,
,
∴△ABE≌△ADN(SAS),
∴∠1=∠2,AE=AN,
∵![]()
∴![]()
∴![]() ,
,
即![]()
∵在△EAM和△NAM中,
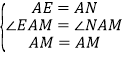 ,
,
∴△EAM≌△NAM(SAS),
又∵EM和NM是对应边,
∴AB=AH(全等三角形对应边上的高相等);
(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,
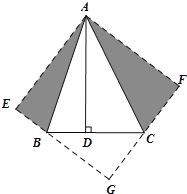
∵AD是△ABC的高,
∴![]()
∴![]()
又∵![]()
∴![]() ,
,
延长EB、FC交于点G,则四边形AEGF是矩形,
又∵AE=AD=AF
∴四边形AEGF是正方形,
由(1)、(2)知:EB=DB=2,FC=DC=3,
设AD=x,则EG=AE=AD=FG=x,
∴BG=x2;CG=x3;BC=2+3=5,
在Rt△BGC中,![]()
解得![]()
故AD的长为6.

【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射靶![]() 次,将射击结果作统计分析如下:
次,将射击结果作统计分析如下:
命中环数 |
|
|
|
|
|
| 平均数 | 众数 | 方差 | |
甲命中环数的次数 |
|
|
|
|
|
|
|
|
| |
乙命中环数的次数 |
|
|
|
|
|
| ________ | ________ | ________ |
![]() 请你完成上表中乙进行射击练习的相关数据;
请你完成上表中乙进行射击练习的相关数据;
![]() 根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.
根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.