题目内容
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是__________________________.

【答案】1.2≤x<2
【解析】证明四边形AEPF是矩形,求出![]() 求出
求出![]() ,即可得出答案.
,即可得出答案.
连接AP. ∠BAC=90°,AB=3,AC=4,
![]()
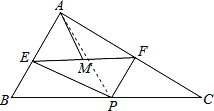
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=∠BAC=90
∴四边形AEPF是矩形,
∴AP=EF,
∵![]() ,M为EF中点,
,M为EF中点,
∴![]() 当AP⊥BC时,AP值最小,
当AP⊥BC时,AP值最小,
此时![]()
AP=2.4,
即AP的范围是![]()
∴![]()
∴AM的范围是![]() (即
(即![]() ).
).
综上所述,x的取值范围是:![]()
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目