题目内容
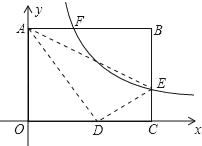
【题目】矩形OABC在平面直角坐标系中如图,已知AB=10,BC=8,EB是C上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() (k>0)与AB相交于点F,则线段AF的长为( )
(k>0)与AB相交于点F,则线段AF的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】B
【解析】
首先根据折叠的性质得到BE=DE,AB=AD,∠ABE=∠ADE=90°,然后利用勾股定理求得OD的长,从而得到DC=OCOD=106=4,设点E的坐标为![]() 则可以表示
则可以表示![]() 然后在Rt△ECD中,利用勾股定理
然后在Rt△ECD中,利用勾股定理![]() 解得k值后即可求得反比例函数的解析式,代入y=8后求得x的值即可求得AF.
解得k值后即可求得反比例函数的解析式,代入y=8后求得x的值即可求得AF.
∵将△ABE沿AE折叠,点B刚好与OC边上点D重合,
∴BE=DE,AB=AD,∠ABE=∠ADE=90°,
∵AB=10,BC=8,
∴AO=BC=8,AD=AB=10,
∴由勾股定理得:![]()
∴DC=OCOD=106=4,
设点E的坐标为![]()
∴![]()
在Rt△ECD中,
![]() 即:
即:![]()
解得:k=30,
∴反比例函数的解析式是![]()
令y=8,
解得:![]()
∴![]()
故选B.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目