题目内容
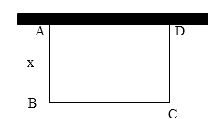
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

【答案】不能并排裁出两个面积均为147cm2的圆,理由见解析.
【解析】分析:根据长方形的长宽比设长方形的长DC为3xcm,宽AD为2xcm,结合长方形ABCD的面积为300cm![]() ,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积147cm
,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积147cm![]() ,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
本题解析:设长方形的长DC为3xcm,宽AD为2xcm.
由题意,得 3x2x=300,
∵x>0,
∴![]() ,
,
∴AB=![]() cm,BC=
cm,BC=![]() cm.
cm.
∵圆的面积为147cm2,设圆的半径为rcm,
∴πr2=147,
解得:r=7cm.
∴两个圆的直径总长为28cm.
∵![]() ,
,
∴不能并排裁出两个面积均为147cm2的圆.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目