Question

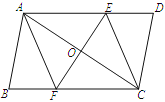
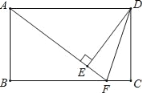
【题目】如图，已知矩形ABCD中，F是BC上一点，且AF＝BC，DE⊥AF，垂足是E，连接DF．求证：

（1）△ABF≌△DEA；

（2）DF是∠EDC的平分线．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据矩形性质得出∠B＝90°，AD＝BC，AD∥BC，推出∠DAE＝∠AFB，求出AF＝AD，根据AAS证出即可；

（2）有全等推出DE＝AB＝DC，根据HL证△DEF≌△DCF，根据全等三角形的性质推出即可．

（1）∵四边形ABCD是矩形，

∴∠B＝90°，AD＝BC，AD∥BC，

∴∠DAE＝∠AFB，

∵DE⊥AF，

∴∠DEA＝∠B＝90°，

∵AF＝BC，

∴AF＝AD，

在△DEA和△ABF中

∵

∴△DEA≌△ABF（AAS）；

（2）证明：∵由（1）知△ABF≌△DEA，

∴DE＝AB，

∵四边形ABCD是矩形，

∴∠C＝90°，DC＝AB，

∴DC＝DE．

∵∠C＝∠DEF＝90°

∴在Rt△DEF和Rt△DCF中

∴Rt△DEF≌Rt△DCF（HL）

∴∠EDF＝∠CDF，

∴DF是∠EDC的平分线．