题目内容
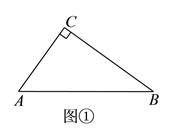
【题目】如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.
求证:(1)DF=AB;
(2)DE是∠FDC的平分线.
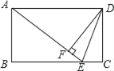
【答案】(1)见解析;(2)见解析.
【解析】
(1)由矩形的性质得出AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,得出∠DAF=∠AEB,证出AD=AE,由AAS证明△ADF≌△EAB,即可得出结论;
(2)由HL证明Rt△DEF≌Rt△DEC,得出对应角相等∠EDF=∠EDC,即可得出结论.
(1)∵四边形ABCD是矩形,
∴AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,
∴∠DAF=∠AEB,
∵AE=BC,
∴AD=AE,
∵DF⊥AE,
∴∠AFD=∠DFE=90°,
∴∠AFD=∠B,
在△ADF和△EAB中, 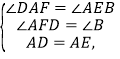
∴△ADF≌△EAB(AAS),
∴DF=AB;
(2)∵DF=AB,AB=DC,
∴DF=DC,
在Rt△DEF和Rt△DEC中, ![]()
∴Rt△DEF≌Rt△DEC(HL),
∴∠EDF=∠EDC,
∴DE是∠FDC的平分线.

【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?