题目内容
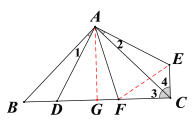
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

【答案】(1)证明见解析;(2)BD2+FC2=DF2,理由见解析;(3)![]() .
.
【解析】
(1)根据垂直的定义以及直角,得到∠BAD=∠CAE,然后SAS证明即可;
(2)根据等腰直角三角形的性质得到∠B=∠ACB=45°,然后由(1)的结论得到∠ACE=45°,BD=CE,从而得到∠FCE=90°,根据勾股定理得出![]() ,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
(3)过点A作![]() 于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
(1)∵![]()
∴![]()
又∵![]()
∴![]()
在△ABD和△ACE中
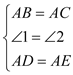
∴△ABD≌△ACE;
(2)![]() 理由如下:
理由如下:
连接FE, ∵![]()
∴![]()
由(1)知△ABD≌△ACE
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵AF平分![]()
∴![]()
在△DAF和△EAF中
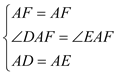
∴△DAF≌△EAF
∴![]() .
.
∴![]() ;
;
(3)过点A作![]() 于G
于G
由(2)知![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴在![]() 中
中![]() .
.

练习册系列答案
相关题目