题目内容
【题目】已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
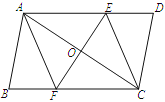
(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
【答案】(1)证明见解析;(2)EF⊥AC.
【解析】试题分析:此题主要考查了平行四边形的性质,以及全等三角形的判定和性质,关键是掌握平行四边形的对边相等;平行四边形的对角相等.
(1)首先根据平行四边形的性质可得AB=CD,∠B=∠D,AD=BC,AD∥BC,然后证明△AOE≌△COF,可得CF=AE,再证明DE=BF,进而可证明△ABF≌△CDE;
(2)在证明△AOE≌△COF的过程中,只需要∠AOE=∠FOC,对顶角相等即可,无需垂直,因此EF⊥AC是多余条件.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO,
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF;
(2)EF⊥AC.

练习册系列答案
相关题目
