题目内容
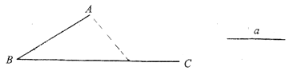
【题目】(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB,AD,DC之间的等量关系______.
(2)同题探究.
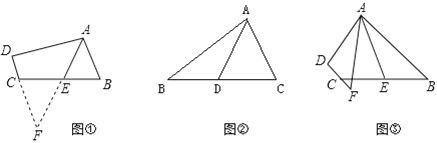
①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
【答案】(1)AD=AB+DC;(2)①1<AD<5;②AB=AF+CF,证明见解析.
【解析】
(1)利用平行线的性质及角平分线的定义,易证∠BAE=∠F,∠BAE=∠DAF,从而可以推出∠F=∠DAF,再利用等角对等边,可证AD=DF,利用线段中点的定义,可知BE=CE,然后利用AAS证明△ABE≌△FCE,利用全等三角形的对应边相等,可证得AB=CF,再根据DF=DC+CF,可得AB,AD,DC之间的数量关系;
(2)①延长AD至E,使DE=AD,连结BE,利用SAS证得△ADC≌△EDB,根据全等三角形的性质,可得AC=BE,由此将AD,AB,AC转化到一个三角形中,然后利用三角形的三边关系定理,即可求出AD的取值范围;②延长AE交DF的延长线于点G,根据已知易得CE=BE,∠BAE=∠G,再利用 AAS证明△AEB≌△GEC,利用全等三角形的对应边相等可证得AB=GC,然后利用角平分线的定义推出∠FAG=∠G,从而可得到FA=FG,然后根据CG=CF+FG,可证得结论.
解:(1)AD=AB+DC;
理由:延长AE交DC的延长线于点F,
∵AB∥CD,AE平分∠DAB,
∴∠BAE=∠F,∠BAE=∠DAF,
∴∠F=∠DAF,
∴AD=DF,
∵点E是CB的中点,
∴BE=CE,
在△ABE和△FCE中,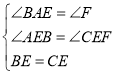 ,
,
∴△ABE≌△FCE(AAS),
∴AB=CF,
∵AD=DF=DC+CF,
∴AD=AB+DC;
(2)①延长AD至E,使DE=AD,连结BE,
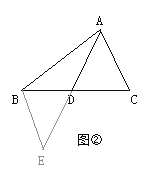
∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,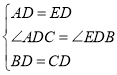 ,
,
∴△ADC≌△EDB(SAS),
∴AC=BE,AE=2AD,
在△ABE中,AB-BE<AE<AB+BE,
∴2<2AD<10,
∴1<AD<5;
②AB=AF+CF;
证明:延长AE交DF的延长线于点G,
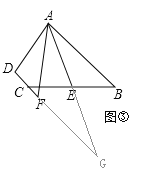
∴E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G,
在△AEB和△GEC中,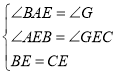 ,
,
∴△AEB≌△GEC,
∴AB=GC,
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG,
∵∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∵CG=CF+FG,
∴AB=AF+CF.

 阅读快车系列答案
阅读快车系列答案