题目内容
【题目】如图，在平面直角坐标系
中，A(- 1,5)，B(- 1,0)，C(- 4,3)．
（1）求出△ABC的面积；
（2）在图中作出△ABC关于
轴的对称图形△A1B1C1；
（3）设P是y轴上的点，要使得点P到点A，C的距离和最小，求点P的坐标．
【答案】（1）
；（2）见解析；（3）
【解析】
（1）根据三角形的面积公式可得答案；
（2）根据关于y轴对称的点的坐标特点：纵坐标不变，横坐标互为相反数可得点A1，B1，C1的坐标；
（3）连接AC1，利用待定系数法求AC1所在直线解析式，令x=0即可得出答案．
（1）△ABC的面积=
×5×3＝；
（2）如图所示：
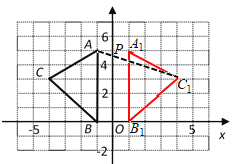
△A1B1C1即为所求.
（3）根据题意得，A（-1，5），C1（4，3）
连接AC1交y轴于点P，
设AC1所在直线解析式为：y=kx+b，
将A（-1，5），C1（4，3）代入y=kx+b得：
，
解得，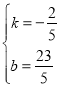
，
∴AC1所在直线解析式为：
，
令x=0，则y=
，
∴P（0，）.
练习册系列答案
名校课堂系列答案
相关题目
