题目内容
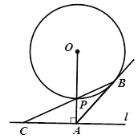
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),△ABO绕点B顺时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
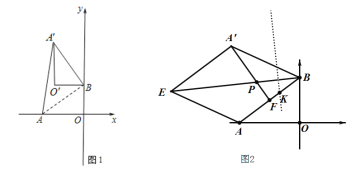
(1)如图1,若α=90°,求AA′的长;
(2)在(1)的条件下,边OA上的一点M旋转后的对应点为N,当O′M+BN取得最小值时,在图中画出求点M的位置,并求出点N的坐标。
(3)如图2,在△ABO绕点B顺时针旋转过程中,以AB、A′B为邻边画菱形AB A′E,F是AB的中点,连A′F交BE于P,BP的垂直平分线交AB于K,当α从60°到90°的变化过程中,点K的位置是否变化?若不变,求BK的长并直接写出此变化过程中点P的运动路径长.
【答案】(1)AA'=![]() ;(2)作图见解析,N(﹣3,
;(2)作图见解析,N(﹣3,![]() );(3)不发生变化,
);(3)不发生变化,![]()
【解析】
(1)先求出AB的长度,然后利用旋转的性质得到![]() ,然后得到
,然后得到![]() 的长度;
的长度;
(2)根据题意,利用轴对称的性质,先确定出点M的位置,然后求出点M的坐标,利用旋转的性质,即可得到点N的坐标;
(3)根据菱形的性质,得到△FBP∽△A′EP,然后结合相似三角形的性质和平行线分线段成比例,求出BK的长度;根据弧长公式,即可求出点P的运动路径长.
解:(1)∵A(﹣4,0),点B(0,3),
∴OA=4,OB=3
由勾股定理得:AB=![]() ,
,
∵旋转角![]() =90°,
=90°,
由旋转知A'B=AB=5,
∴△A'BA是等腰直角三角形,
∴AA'=![]() ;
;
(2)由旋转知BN=BM,
∴O′M+BN的最小值=O′M+BM的最小值,
∴作出点B(0,3)关于x轴的对称点B'(0,﹣3),连接O'B'交OA于点M,点M即为所求;
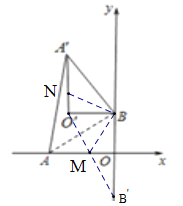
设O′B':y=kx+b把O′(﹣3,3)B'(0,﹣3)代入得
![]() ,
,
解得:k=﹣2,b=﹣3,
∴O′B'为y=﹣2x﹣3;
令'y=0得:x=﹣![]() ,
,
∴M(﹣![]() ,0),MO =
,0),MO =![]() ,
,
∵由旋转的性质得△BOM≌△BO′N,
∴OM =O′N=![]() ,
,
∴N的纵坐标为:3+![]() =
=![]() ,
,
∴N(﹣3,![]() );
);
(3)不发生变化;理由如下:
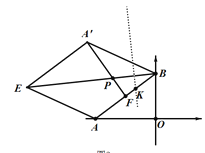
∵F是BC的中点,
∴BF=AF=![]() AB,
AB,
∵四边形AB A′E是菱形,
∴AB=A′E,AB∥A′E,
∴△FBP∽△A′EP,
∴![]() ,
,
∵四边形AB A′E是菱形,
∴∠ABE=∠A′ BE,
又∵BP的中垂线与边AB交于点K,
∴KP=KB,
∴∠ABE=∠KPB,
∴∠KPB=∠A′ BE,
∴PK∥AE∥A′ B,
∴![]() ,
,
∴BK=![]() AB=
AB=![]() ,
,
即点K的位置不发生改变;
∴P点经过路线是以K为圆心,BK为半径的圆弧,
长度为: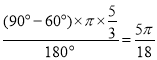 .
.