��Ŀ����
��ͼ�������� ��x�ύ�ڵ�A����2��0������y���ڵ�B��0��
��x�ύ�ڵ�A����2��0������y���ڵ�B��0�� ��.ֱ
��.ֱ ����A��y�ύ�ڵ�C���������ߵ���һ��������D.
����A��y�ύ�ڵ�C���������ߵ���һ��������D.
��1���������� ��ֱ��
��ֱ�� �Ľ���ʽ��
�Ľ���ʽ��
��2�����P��ֱ��AD�·�����������һ���㣨�����A��D�غϣ�������P�� y���ƽ���ߣ���ֱ��AD�ڵ�M����DE��y���ڵ�E��̽�����Ƿ���������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ��������������P�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£���PN��AD�ڵ�N�����PMN���ܳ�Ϊm����P�ĺ�����Ϊx����m��x�ĺ�����ϵʽ�������m�����ֵ��
��1�� ,
, ;��2������,��2����3���ͣ�4��
;��2������,��2����3���ͣ�4�� ��;��3��
��;��3�� ,��x=3ʱ��m�����ֵ��15.
,��x=3ʱ��m�����ֵ��15.
���������������1����A��B��������ֱ����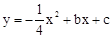 ������κ�������ʽ����A���������
������κ�������ʽ����A��������� ���ֱ�߽���ʽ;
���ֱ�߽���ʽ;
��2�����ȼ����P��M������꣬�����ó�PM�ij����������������ó�D�����꣬�����ó�CE�ij�������ƽ���ı��ε��ж��ó�PM=CE���ó���ʽ�����������;
��3�����ù��ɶ����ó�DC�ij����������ݡ�PMN�ס�CDE���ó����������ܳ�֮�ȣ����m��x�ĺ�����ϵ���������䷽��������κ�����ֵ����.
�����������1���� ������A����2��0����B��0��
������A����2��0����B��0�� ��
��
�� �����
����� .
.
�������ߵĽ���ʽ�� .
.
��ֱ�� ������A����2��0������
������A����2��0������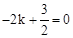 ����ã�
����ã�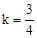 .
.
��ֱ�ߵĽ���ʽ�� .
.
��2������.
��P�������ǣ�x��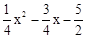 ������M�������ǣ�x��
������M�������ǣ�x��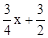 ����
����
�� .
.
�ⷽ��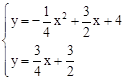 �ã�
�ã�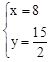 ��
��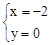 .
.
�ߵ�D�ڵ������ޣ����D�������ǣ�8��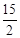 ��.
��.
�� ��x=0�õ�C�������ǣ�0��
��x=0�õ�C�������ǣ�0�� ��.
��.
��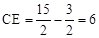 .
.
��PM��y�ᣬ��Ҫʹ�ı���PMEC��ƽ���ı��Σ�����PM=CE����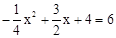 .
.
��������̵ã�x1=2��x2=4.
��x=2ʱ��y="��3;" ��x=4ʱ��y= .
.
��ֱ��AD�Ϸ����������ϴ��������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ���P�������ǣ�2����3���ͣ�4�� ��.
��.
��3����Rt��CDE�У�DE=8��CE=6 �ɹ��ɶ����ã�DC=10.
���CDE���ܳ���24.
��PM��y�ᣬ���PMN=��DCE.
�ߡ�PNM=��DEC�����PMN�ס�CDE.
�� ����
����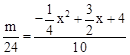 .
.
���������ã�m��x�ĺ�����ϵʽ�ǣ� .
.
�� ��0����m�����ֵ����x=3ʱ��m�����ֵ��15.
��0����m�����ֵ����x=3ʱ��m�����ֵ��15.
���㣺1.���κ����ۺ���;2.����������;3.�����ϵ�������뷽�̵Ĺ�ϵ;4.ƽ���ı��ε��ж�;5.���ɶ���;6.���������ε��ж�������;7.��ʵ�������к�����ϵʽ;8.���κ�������ֵ.


 ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0,4����DΪOC���е�.
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��0,4����DΪOC���е�.
 �������ڣ������G�����ꣻ����������˵�����ɣ�
�������ڣ������G�����ꣻ����������˵�����ɣ� ��ͼ����x�ύ�ڵ�A��-1, 0������y�ύ�ڵ�C��0��-5�����Ҿ�����D��3��-8��.
��ͼ����x�ύ�ڵ�A��-1, 0������y�ύ�ڵ�C��0��-5�����Ҿ�����D��3��-8��.

 ������.
������. ��������
��������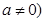 .
. Ϊ��ֵ���ú�����ͼ����
Ϊ��ֵ���ú�����ͼ���� ���������������㣻
���������������㣻
