题目内容
用简便方法计算
(1)20102-2011×2009;
(2)(1-
)(1-
)(1-
)…(1-
)(1-
)
(1)20102-2011×2009;
(2)(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 92 |
| 1 |
| 102 |
考点:平方差公式
专题:计算题
分析:(1)原式变形后,利用平方差公式计算即可得到结果;
(2)原式各括号中利用平方差公式变形,计算即可得到结果.
(2)原式各括号中利用平方差公式变形,计算即可得到结果.
解答:解:(1)原式=20102-(2010+1)×(2010-1)=20102-20102+1=1;
(2)原式=(1+
)(1-
)(1+
)(1-
)…(1+
)(1-
)=
×
×
×
×…×
×
=
.
(2)原式=(1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 9 |
| 10 |
| 11 |
| 10 |
| 11 |
| 20 |
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在3,-
,0,2这四个数中,最小的一个数是( )
| 3 |
| A、3 | ||
B、-
| ||
| C、0 | ||
| D、2 |
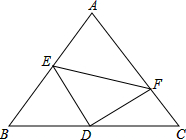 在等腰直角三角形中,AB=AC,点D是BC的中点,点E、F分别为AB,AC边上的点,且DE⊥DF.
在等腰直角三角形中,AB=AC,点D是BC的中点,点E、F分别为AB,AC边上的点,且DE⊥DF. 已知:如图,AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=40°,求∠BHF的度数.
已知:如图,AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=40°,求∠BHF的度数.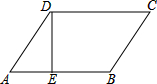 如图,在?ABCD中,DE⊥AB,E是垂足,∠C=40°,求∠A及∠CDE的度数.
如图,在?ABCD中,DE⊥AB,E是垂足,∠C=40°,求∠A及∠CDE的度数.