题目内容
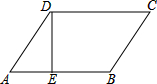如图，在?ABCD中，DE⊥AB，E是垂足，∠C=40°，求∠A及∠CDE的度数．考点：平行四边形的性质
专题：计算题
分析：根据平行四边形的性质：对角相等可求出∠A的度数，再根据同旁内角互补即可求出∠CDE的度数．
解答：解：∵四边形ABCD是平行四边形，
∴∠A=∠C=40°，
∵DE⊥AB，
∴∠DEA=∠DEB=90°，
∵AB∥DC，
∴∠CDE+∠DEB=180°，
∴∠CDE=90°．
故∠A为40°；∠CDE为90°．
∴∠A=∠C=40°，
∵DE⊥AB，
∴∠DEA=∠DEB=90°，
∵AB∥DC，
∴∠CDE+∠DEB=180°，
∴∠CDE=90°．
故∠A为40°；∠CDE为90°．
点评：本题考查了平行四边形的性质、垂直的定义已经平行线的性质，题目的综合性较强，难度不大．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
平行四边形ABCD中，BG垂直于CD，且AB=BG=BE，AE交BG于点F．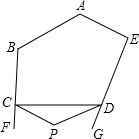 
如图，五边形ABCDE中，∠BCD、∠EDC的外角分别是∠FCD、∠GDC，CP、DP分别平分∠FCD和∠GDC且相交于点P，若∠A=140°，∠B=120°，∠E=90°，∠P=