题目内容
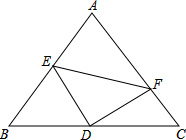 在等腰直角三角形中,AB=AC,点D是BC的中点,点E、F分别为AB,AC边上的点,且DE⊥DF.
在等腰直角三角形中,AB=AC,点D是BC的中点,点E、F分别为AB,AC边上的点,且DE⊥DF.(1)求证:BE2+CF2=EF2;
(2)若BE=12,CF=5,试求△DEF的面积.
考点:全等三角形的判定与性质,等腰三角形的性质,勾股定理
专题:计算题
分析:(1)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到撒尿性EDF和三角形PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证;
(2)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC-CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
(2)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC-CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
解答:解:(1)延长ED到P,使DP=DE,连接FP,CP,
在△BED和△CPD中,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CPD,
在△EDF和△PDF中,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴EF2=BE2+CF2;
(2)连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
,
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC-FC=AB-CF=17-5=12,
在Rt△EAF中,根据勾股定理得:EF=
=13,
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=
,即DE=DF=
,
则S△DEF=
DE•DF=
.
在△BED和△CPD中,
|
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CPD,
在△EDF和△PDF中,
|

∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴EF2=BE2+CF2;
(2)连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
|
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC-FC=AB-CF=17-5=12,
在Rt△EAF中,根据勾股定理得:EF=
| AE2+AF2 |
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=
13
| ||
| 2 |
13
| ||
| 2 |
则S△DEF=
| 1 |
| 2 |
| 169 |
| 4 |
点评:此题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
某星球直径约56700000米,用科学记数法表示正确的为( )
| A、567×105米 |
| B、5.67×105米 |
| C、5.67×107米 |
| D、0.567×108米 |
 如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )