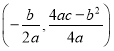题目内容
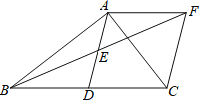
【题目】如图所示,![]() 均为等边三角形,边长分别为
均为等边三角形,边长分别为![]() ,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
①![]() ②
②![]() ③
③![]() 为等边三角形 ④
为等边三角形 ④![]() ⑤CM平分
⑤CM平分![]()
【答案】①②③⑤
【解析】
①根据等边三角形的性质得CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,则∠ACE=60°,利用“SAS”可判断△ACD≌△BCE,则AD=BE;
②过E作![]() ,根据等边三角形求出ED、CN的长,即可求出BE的长;
,根据等边三角形求出ED、CN的长,即可求出BE的长;
③由等边三角形的判定得出△CMN是等边三角形;
④证明△DMC∽△DBA,求出CM长;
⑤证明M、F、C、G四点共圆,由圆周角定理得出∠BMC=∠FGC=60°,∠CMD=∠CFG=60°,得出∠BMC=∠DMC,所以CM平分∠BMD.
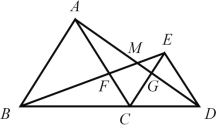
解:连接MC,FG,过点E作EN⊥BD,垂足为N,
①∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACE=60°,
∴∠ACD=∠BCE=120°,
在△ACD和△BCE中,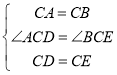
∴△ACD≌△BCE(SAS),
∴AD=BE;①正确;
②∵△CDE都是等边三角形,且边长为3cm.
∴CN=![]() cm,EN=
cm,EN=![]() cm.
cm.
∵BC=5cm.
∴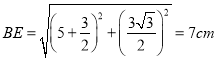 ,②正确;
,②正确;
③∵△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACG和△BCF中,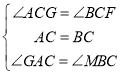
∴△ACG≌△BCF(ASA),
∴CG=CF
而∠GCF=60°,
∴△CFG是等边三角形,③正确;
⑤∵∠EMD=∠MBD+∠MDB=∠MAC+∠MDB=60°=∠FCG,
∴M、F、C、G四点共圆,
∴∠BMC=∠FGC=60°,∠CMD=∠CFG=60°,
∴∠BMC=∠DMC,
∴CM平分∠BMD,⑤正确;
④∵∠DMC=∠ABD,∠MDC=∠BDA
∴△DMC∽△DBA
∴![]()
∴![]()
∴CM=![]() .④错误.
.④错误.
故答案为:①②③⑤.


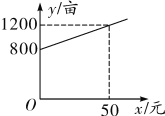
【题目】某校准备组织师生共60人,从甲地乘动车前往乙地参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)求参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,后续前往的教师和学生均购买二等座票.设提早前往的教师有![]() 人,购买一、二等座票全部费用为
人,购买一、二等座票全部费用为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若购买一、二等座票全部费用不多于1030元,则提早前往的教师最多只能有多少人?