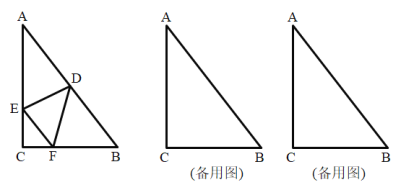
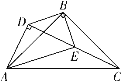
题目内容
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() 且
且![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() 和
和![]() ,并且
,并且![]() .
.
(观察猜想)
(1)如图①,当![]() 时,线段
时,线段![]() 与
与![]() 的数量关系为_____,线段
的数量关系为_____,线段![]() 的数量关系为_______________;
的数量关系为_______________;
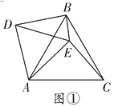
(探究证明)
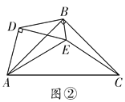
(2)如图②,当![]() 时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
(拓展应用)
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)结论不成立,
;(2)结论不成立,![]() ,见解析;(3)2
,见解析;(3)2
【解析】
(1)猜想![]() ,
,![]() .观察可得
.观察可得![]() 和
和![]() 分别在
分别在![]() 和
和![]() 中,根据已知条件和角的和差关系可证明
中,根据已知条件和角的和差关系可证明![]() ,即可得到
,即可得到![]() ;将线段
;将线段![]() 通过相等的线段转化到
通过相等的线段转化到![]() 中,再通过等角的代换证得
中,再通过等角的代换证得![]() 是直角三角形,进而通过勾股定理证得线段
是直角三角形,进而通过勾股定理证得线段![]() ,
,![]() ,
,![]() 之间的数量关系;(2)观察可得
之间的数量关系;(2)观察可得![]() 和
和![]() 分别在
分别在![]() 和
和![]() 中,根据已知条件和角的和差关系可证明
中,根据已知条件和角的和差关系可证明![]() ,进而得到
,进而得到![]() 和
和![]() 之间的数量关系;同(1)即可证得线段
之间的数量关系;同(1)即可证得线段![]() 之间的数量关系;(3)画出图形,利用(2)中的结论和已知条件即可求解.
之间的数量关系;(3)画出图形,利用(2)中的结论和已知条件即可求解.
解:(1)![]() ;
;![]() ;
;
[解法提示]∵![]() ,
,![]() ,
,
∴![]() ,
,![]() 都是等边三角形,∴
都是等边三角形,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,∴
,∴![]() ,
,
∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)(1)中的结论不成立,正确的结论为:![]() ,
,![]() ;
;
理由如下:∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即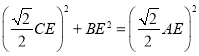 ,则
,则![]() ;
;
(3)2
[解法提示]如图,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵点![]() 在一条直线上,
在一条直线上,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
则![]() .
.

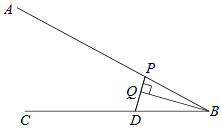
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.