��Ŀ����
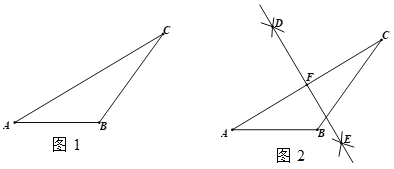
����Ŀ����ͼ����MON=60����OFƽ�֡�MON����A������OM�ϣ� P��Q������ON�ϵ������㣬��P�ڵ�Q����࣬��PQ=OA�����߶�OQ�Ĵ�ֱƽ���ߣ��ֱ�OM��OF��ON�ڵ�D��B��C������AB��PB��
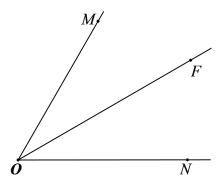
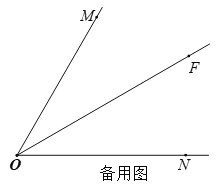
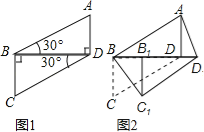
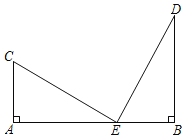
��1�������ⲹȫͼ�Σ�
��2���ж��߶� AB��PB֮���������ϵ����֤����
��3������AP����![]() ����P��Q���㶼������ON���ƶ�ʱ��
����P��Q���㶼������ON���ƶ�ʱ��![]() �Ƿ������Сֵ�������ڣ���ֱ��д��
�Ƿ������Сֵ�������ڣ���ֱ��д��![]() ����Сֵ���������ڣ���˵�����ɣ�
����Сֵ���������ڣ���˵�����ɣ�
���𰸡���1����ȫͼ�μ������� ��2��AB=PB��֤������������3�����ڣ�![]() ��
��
��������
��1���������ⲹȫͼ����ͼ1��
��2�����ۣ�AB=PB������BQ��ֻҪ֤����AOB�ա�PQB���ɽ�����⣻
��3������BQ��ֻҪ֤����ABP�ס�OBQ�������Ƴ�![]() ���ɡ�AOB=30�����Ƴ���BA��OMʱ��
���ɡ�AOB=30�����Ƴ���BA��OMʱ��![]() ��ֵ��С����СֵΪ
��ֵ��С����СֵΪ![]() ���ɴ˼��ɽ�����⣮
���ɴ˼��ɽ�����⣮
�⣺��1����ͼ1��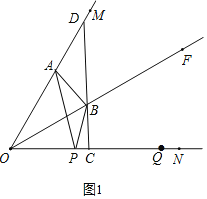
��2��AB=PB��
֤������ͼ������BQ��
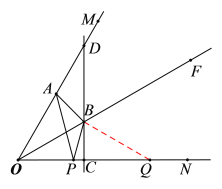
��BC�Ĵ�ֱƽ��OQ��
�� OB =BQ��
���BOP=��BQP��
�֡� OFƽ�֡�MON��
���AOB = ��BOP��
���AOB = ��BQP��
�֡�PQ=OA��
�� ��AOB�ա�PQB��
��AB=PB��
��3�����ߡ�AOB�ա�PQB��
���OAB=��BPQ��
�ߡ�OPB+��BPQ=180����
���OAB+��OPB=180������AOP+��ABP=180����
�ߡ�MON=60����
���ABP=120����
��BA=BP��
���BAP=��BPA=30����
��BO=BQ��
���BOQ=��BQO=30����
���ABP�ס�OBQ��
��![]() ��
��
�ߡ�AOB=30����
�൱BA��OMʱ��![]() ��ֵ��С����СֵΪ
��ֵ��С����СֵΪ![]() ��
��
��k=![]() ��
��