题目内容
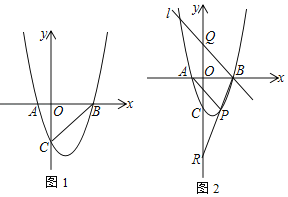
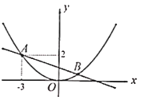
【题目】已知二次函数图象的顶点在原点
，对称轴为
轴.直线
的图象与二次函数的图象交于点
和点
（点
在点
的左侧）
（1）求
的值及直线
解析式；
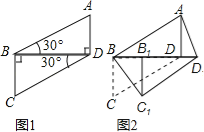
（2）若过点
的直线
平行于直线且直线与二次函数图象只有一个交点
，求交点的坐标.
【答案】（1）m=
，
；（2）
【解析】
（1）由于抛物线的顶点为原点，因此可设其解析式为y=ax2，直接将A点，B点的坐标代入抛物线中即可求出抛物线的解析式以及m的值，进而可知出点B的坐标，再将A，B点的坐标代入一次函数中，即可求出一次函数的解析式．
（2）根据题意可知直线l2的解析式
，由抛物线与l2只有一个交点，联立直线
与二次函数的解析式，消去y，得出一个含x一元二次方程，根据方程的判别式为0可求得n的值，进而得出结果．
（1）解：假设二次函数的解析式为
，
将
分别代入二次函数的解析式，
得：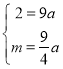
，解得
．
解得：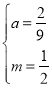
．
将
代入
中，
得
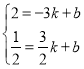，,解得：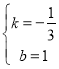
．
的解析式为．
（2）由题意可知：l2∥l1，
可设直线的解析式为：
过点
，则有：
．
．
由题意，联立直线与二次函数的解析式，可得以下方程组：
，
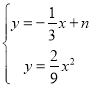消元，得：
，
整理，得：
， ①
由题意，得与
只有一个交点，
可得：
，
解得：
．
将代回方程①中，得
．
将代入
中，
得
．
可得交点
坐标为．
练习册系列答案
相关题目
【题目】九年级（1）班的小华和小红两名学生10次数学测试成绩如下表（表I）所示：
小花 | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
小红 | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
现根据上表数据进行统计得到下表（表Ⅱ）：
姓名 | 平均成绩 | 中位数 | 众数 |
小华 | 80 | ||
小红 | 80 | 90 |
（1）填空：根据表I的数据完成表Ⅱ中所缺的数据；
（2）老师计算了小红的方差
请你计算小华的方差并说明哪名学生的成绩较为稳定．
