题目内容
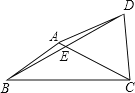
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC。
(1)求证:BE⊥DE;
(2)H是直线CD上一动点(不与D重合),HI平分∠HBD交CD于点I。请你画出图形,并猜想∠EBI与∠BHD的数量关系,且说明理由。
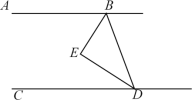
【答案】(1)见解析;(2)当H在点D的左侧时,∠BHD=2∠EBI;当H在点D的右侧时,∠BHD=180°-2∠EBI;理由见解析
【解析】
(1)根据平行线的性质以及角平分线的定义,即可得到BE⊥DE;
(2)根据角平分线的定义可得∠ABD=2∠EBD;∠HBD=2∠DBI,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠BHD,从而得解
(1)证明:过点E作EF∥AB
∴∠ABE=∠BEF
又∵AB∥CD
∴∠ABD+∠BDC=180°,EF∥CD,
∴∠FED=∠CDE
∵BE平分∠ABD,DE平分∠BDC,
∴∠ABE=![]() ∠ADB,∠CDE=
∠ADB,∠CDE=![]() ∠BDC,
∠BDC,
∴∠ABE+∠CDE=![]() ×180°=90°
×180°=90°
∴∠BEF+∠FED=90°,即∠BED=90°
∴BE⊥DE

(2)①当H在点D的左侧时,∠BHD=2∠EBI;
证明:∵AB∥CD
∴∠ABH=∠BHD;
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABD=2∠EBD;∠HBD=2∠DBI;
∠ABH=∠ABD-∠HBD=2(∠EBD-∠DBI)=2∠EBI;
∴∠BHD=2∠EBI;
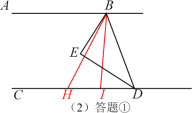
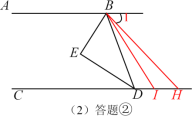
②当H在点D的右侧时,∠BHD=180°-2∠EBI;
证明:∵AB∥CD
∴∠BHD=∠1;
又∵∠1+∠ABH=180°;
∴∠1+∠ABD+∠DBH=180°,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABD=2∠EBD;∠HBD=2∠DBI;
∴∠1+2∠EBD+2∠DBI=180°,
∴∠1=180°-2(∠EBD+∠DBI) =180°-2∠EBI,
即∠BHD=180°-2∠EBI。

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案