题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,垂足为
轴,垂足为![]() ,交线段
,交线段![]() 于点
于点![]() .
.
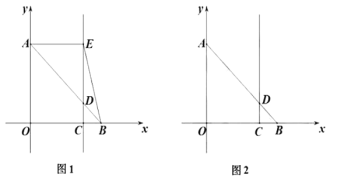
(1)如图1,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
①填空:![]() 的面积为______;②点
的面积为______;②点![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 为线段
为线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,线段
,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出点
,请直接写出点![]() 的坐标为______.
的坐标为______.
【答案】(1)①6;②![]() 的坐标为
的坐标为![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)①易证四边形AECO为矩形,则点B到AE的距离为OA,AE=OC=3,OA=CE=4,S△ABE=![]() AEOA,即可得出结果;
AEOA,即可得出结果;
②设点![]() 的坐标为
的坐标为![]() ,分两种情况: 点
,分两种情况: 点![]() 在点
在点![]() 上方,连接
上方,连接![]() ,得
,得![]() =
=![]() +
+![]() +
+![]() =8,点
=8,点![]() 在点
在点![]() 的下方,得
的下方,得![]() =8,分别列出方程解方程即可得出结果;
=8,分别列出方程解方程即可得出结果;
(2)由S△AOF=S△QBF,则S△AOB=S△QOB,△AOB与△QOB是以AB为同底的三角形,高分别为:OA、QC,得出OA=CQ,即可得出结果.
解:(1)①∵CD⊥x轴,AE⊥CD,
∴AE∥x轴,四边形AECO为矩形,点B到AE的距离为OA,
∵点A(0,4),点C(3,0),
∴AE=OC=3,OA=CE=4,
∴S△ABE=![]() AEOA=
AEOA=![]() ×3×4=6,
×3×4=6,
故答案为:6;
②设点![]() 的坐标为
的坐标为![]() .
.
(i)∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴点![]() 在点
在点![]() 上方,连接
上方,连接![]() (如图1).根据题意得
(如图1).根据题意得

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴当点![]() 的坐标为
的坐标为![]() .
.
(ii)点![]() 在点
在点![]() 的下方,连接
的下方,连接![]() (如图2).
(如图2).
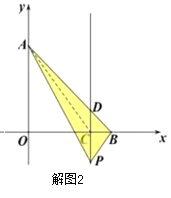
∵![]() .
.
∴![]() .
.
∴点![]() 在点
在点![]() 的下方,根据题意得
的下方,根据题意得
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴当点![]() 的坐标为
的坐标为![]() .
.
(2)(2)∵S△AOF=S△QBF,如图3所示:
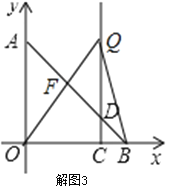
∴S△AOB=S△QOB,
∵△AOB与△QOB是以AB为同底的三角形,高分别为:OA、QC,
∴OA=CQ,
∴点Q的坐标为(3,4),
故答案为:(3,4).

【题目】“母亲节”快到了,七(1)班班委发起慰问烈士家属王大妈和李大妈的活动,决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集资金.已知同学们从花店按每枝1.4元买进鲜花,并按每枝3元卖出,设卖出鲜花x枝.
品名 | 热水壶 | 电饭煲 |
单价(单位:元/只) | 125 | 250 |
(1)每卖出一枝鲜花赚_______元,卖出鲜花x枝赚______元;
(2)若从花店购买鲜花的同时,同学们还花了50元购买包装材料,请把所筹集的资金y(元)用鲜花的销售量x(枝)的代数式表示;现在筹集的资金为750元,问需要卖出鲜花多少枝?
(3)已知两种家用小电器的单价如下表所示,现将筹集的750元全部用于购买表中家用小电器赠送两位大妈,且电饭煲至少要购买1只,请求出所有的购买方案.
【题目】某校为了解学生参加“经典诵读”的活动情况.该校随机选取部分学生,对他们在三、四月份的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
四月份日人均诵读时间的统计表
日人均诵读时间 | 人数 | 百分比 |
| 6 | |
| 30 | |
|
|
|
| 10 |
|
|
|
|
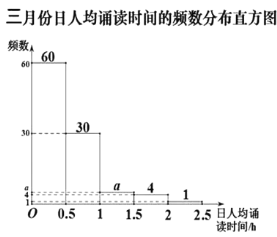
根据以上信息,解答下列问题:
(1)本次调查的学生人数为______;
(2)图表中的![]() ,
,![]() ,
,![]() ,
,![]() 的值分别为______,______,______,______;
的值分别为______,______,______,______;
(3)在被调查的学生中,四月份日人均诵读时间在![]() 范围内的人数比三月份在此范围的人数多______人.
范围内的人数比三月份在此范围的人数多______人.